Joule-Thomson Effect

The Joule-Thomson Effect describes the change in temperature of a real gas or liquid when it is forced through a valve or porous plug while kept insulated so that no heat is exchanged with the environment. This effect is significant in thermodynamics and has practical applications in refrigeration and liquefaction of gases.

What is Joule-Thomson Effect?

The Joule-Thomson Effect refers to the temperature change experienced by a real gas when it is allowed to expand freely through a valve or a porous plug, without any heat exchange with the environment (adiabatic process). This effect is important in understanding the behavior of gases under different conditions and is widely used in refrigeration and gas liquefaction.

According to thermodynamic principles, we can best understand the Joule-Thomson effect by considering a gas packet moving against the flow through a restriction. The upstream gas must perform work to push the gas packet forward through this restriction. This work equals the product of the gas packet’s volume and the upstream pressure.

𝑊₁ = 𝑉ₚₐ꜀ₖₑₜ ₁ ×𝑃₁

As the gas packet moves through the restriction, it needs to create space by displacing some of the downstream gas. This involves performing work that is the product of the packet volume and the downstream pressure.

𝑊₂ = 𝑉ₚₐ꜀ₖₑₜ ₂×𝑃₂

Due to varying compressibility effects, real gases do not have equal work done upstream and downstream. Since this depressurization is an adiabatic process, the system does not exchange heat with the surroundings. Thus, the change in internal energy must adhere to the first law of thermodynamics.

𝑈₂−𝑈₁=𝑊₁−𝑊₂

Gas molecules experience both repulsive and attractive forces (Van der Waals forces) as they are in constant motion. When the gas pressure is reduced, the average distance between the molecules increases, causing the attractive forces to dominate for many gases at room temperature. This dominance results in an increase in potential energy.

Most real gases require more work downstream at ambient temperatures due to compressibility effects.

𝑃₁×𝑉₁<𝑃₂×𝑉₂

This indicates that the internal energy decreases when the gas moves through the restriction.

Generally, for many real gases, the temperature decreases during a pressure drop. However, this is not universal for all gases and conditions. Since the process is isenthalpic (constant enthalpy), the temperature can either decrease or increase depending on how the internal energy changes to maintain constant enthalpy.

Joule Thomson Coefficient

The Joule-Thomson coefficient 𝜇ⱼₜ is defined as the rate of change of temperature 𝑇 with respect to pressure P during a constant enthalpy process:

𝜇ⱼₜ = (∂𝑇/∂𝑃)𝐻

The following table explains when the Joule-Thomson effect cools or warms a real gas:

If the gas temperature is	then 𝜇ⱼₜ​ is	since ∂P is	thus ∂𝑇 must be	So the gas
above the inversion temperature	negative	always negative	positive	warms
below the inversion temperature	positive	always negative	negative	cools

Derivation of Joule-Thomson Effect

The Joule-Thomson coefficient can be derived using thermodynamic relationships and is defined as the change in temperature during an isenthalpic process (constant enthalpy) due to a pressure drop:

𝜇 = (∂𝑇/∂𝑃)𝐻​

Applying the cyclic rule of partial derivatives:

(∂𝑇/∂𝑃)ₕ(∂𝑃/∂𝐻)ₜ(∂𝐻/∂𝑇)ₚ = −1

Since:

(∂𝑃∂𝐻)ₜ = −(∂𝐻∂𝑃)⁻¹ₜ

It follows that:

(∂𝑇/∂𝑃)ₕ = −(∂𝐻/∂𝑃)ₜ(∂𝑇/∂𝐻)ₚ

Since:

(∂𝐻/∂𝑇)ₚ = 𝐶𝑝​

Thus:

𝜇 = 1/𝐶𝑝[𝑇(∂𝑣ˉ/∂𝑇)ₚ−𝑣ˉ ]

Where 𝑣ˉ is the molar volume and 𝐶ₚ​ is the heat capacity at constant pressure. For real gases, this is further expressed as:

𝜇=𝑅𝑇²/𝑃𝐶ₚ(∂𝑍/∂𝑇)ₚ​

This isenthalpic process, described in terms of pressure, temperature, and volume, demonstrates how the Joule-Thomson coefficient relates to the physical properties of the gas.

Temperature Inversion

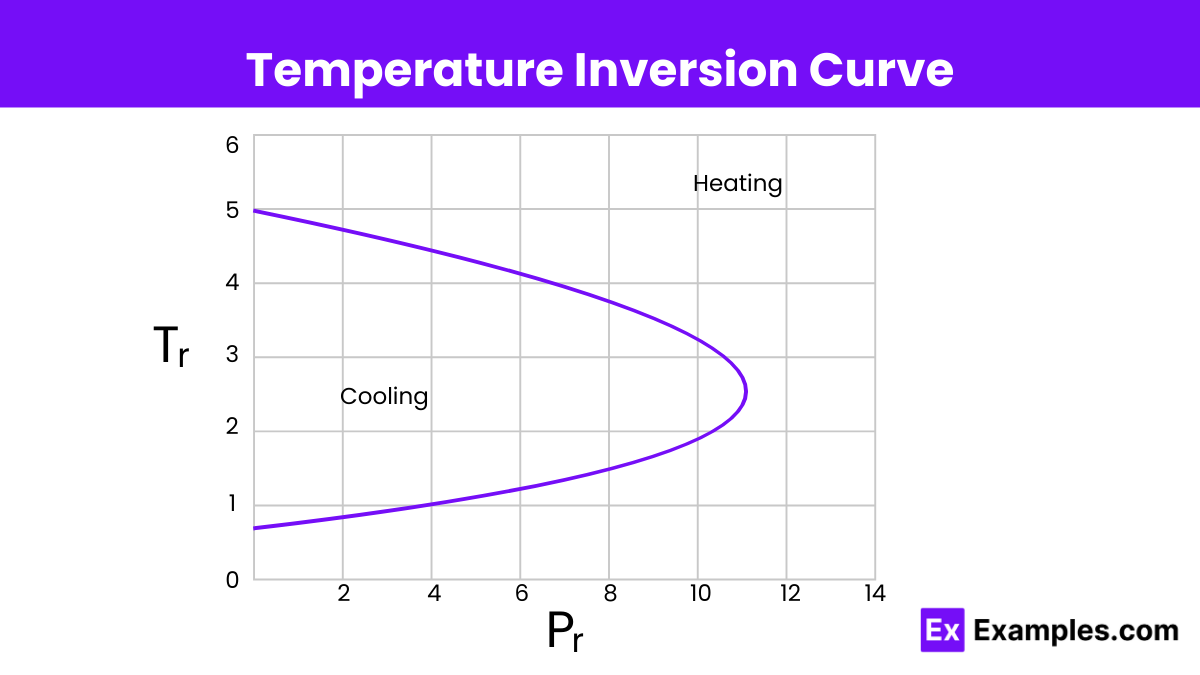
The inversion temperature is the temperature of a gas at which reducing the pressure does not change the temperature. Above this temperature, the gas heats up during expansion, while below this temperature, the gas cools down during expansion.

Uses of Joule-Thomson Effect

• Refrigeration and Liquefaction: You use the Joule-Thomson effect to cool gases in refrigeration systems. By forcing a gas through a throttle, you cause it to expand and cool, which is essential for liquefying gases like oxygen, nitrogen, and natural gas.
• Air Conditioning Systems: You apply the Joule-Thomson effect in air conditioning systems. By allowing refrigerants to expand through a throttle or expansion valve, you achieve the cooling necessary to lower the air temperature in buildings and vehicles.
• Natural Gas Processing: You utilize the Joule-Thomson effect in natural gas processing to remove condensable hydrocarbons. By expanding the natural gas through a valve, you cause it to cool, which leads to the condensation of heavier hydrocarbons, making it easier to separate and purify the gas.
• Hydrogen Production and Storage: You use the Joule-Thomson effect to liquefy hydrogen for storage and transport. By forcing hydrogen gas through an expansion valve, you reduce its temperature significantly, enabling it to reach the liquefaction point.
• Gas Pressure Regulation: You apply the Joule-Thomson effect in gas pressure regulators. As gas expands through the regulator, its temperature changes, which is crucial for maintaining stable pressure and temperature conditions in various industrial processes.
• Cryogenics: You exploit the Joule-Thomson effect in cryogenic applications to achieve extremely low temperatures. By expanding gases like helium and nitrogen, you produce the cooling necessary for scientific research, including superconductivity studies and the preservation of biological samples.

Examples for Joule-Thomson Effect

1. Refrigeration and Air Conditioning: In refrigeration systems, you use the Joule-Thomson effect to cool refrigerants. When a high-pressure refrigerant expands through an expansion valve, it undergoes a temperature drop.
2. Liquefaction of Gases: You apply the Joule-Thomson effect to liquefy gases like oxygen, nitrogen, and natural gas. By forcing these gases through a valve under high pressure and then allowing them to expand, you achieve the cooling required for their liquefaction.
3. Natural Gas Processing: In natural gas plants, you use the Joule-Thomson effect to remove heavier hydrocarbons from natural gas. By expanding the gas through a valve, you cool it, causing heavier hydrocarbons to condense. This separation process is vital for producing clean, dry natural gas.
4. Hydrogen Production and Storage: You employ the Joule-Thomson effect to liquefy hydrogen for storage and transportation. By expanding hydrogen gas through an expansion valve, you achieve the low temperatures necessary for liquefaction. This is critical for the efficient storage and transport of hydrogen as a fuel.
5. Cryogenic Applications: In cryogenics, you use the Joule-Thomson effect to reach extremely low temperatures. For example, you can cool helium gas by expanding it through a throttle to achieve the temperatures needed for superconductivity research or the preservation of biological samples.
6. Gas Pressure Regulation: You utilize the Joule-Thomson effect in gas pressure regulators. As gas expands through a pressure regulator, its temperature changes. This temperature change helps maintain stable pressure and temperature conditions in various industrial applications, ensuring safe and efficient operations.
7. Thermodynamic Studies: Researchers use the Joule-Thomson effect to study the thermodynamic properties of gases. By observing how gases respond to expansion and cooling, scientists gain insights into their intermolecular forces and behavior under different conditions, enhancing our understanding of gas dynamics.
8. Heat Pumps: In heat pumps, you use the Joule-Thomson effect to transfer heat from one place to another. By expanding the working fluid through an expansion valve, you achieve the cooling needed to absorb heat from the environment, which is then released at a different location.

FAQ’s