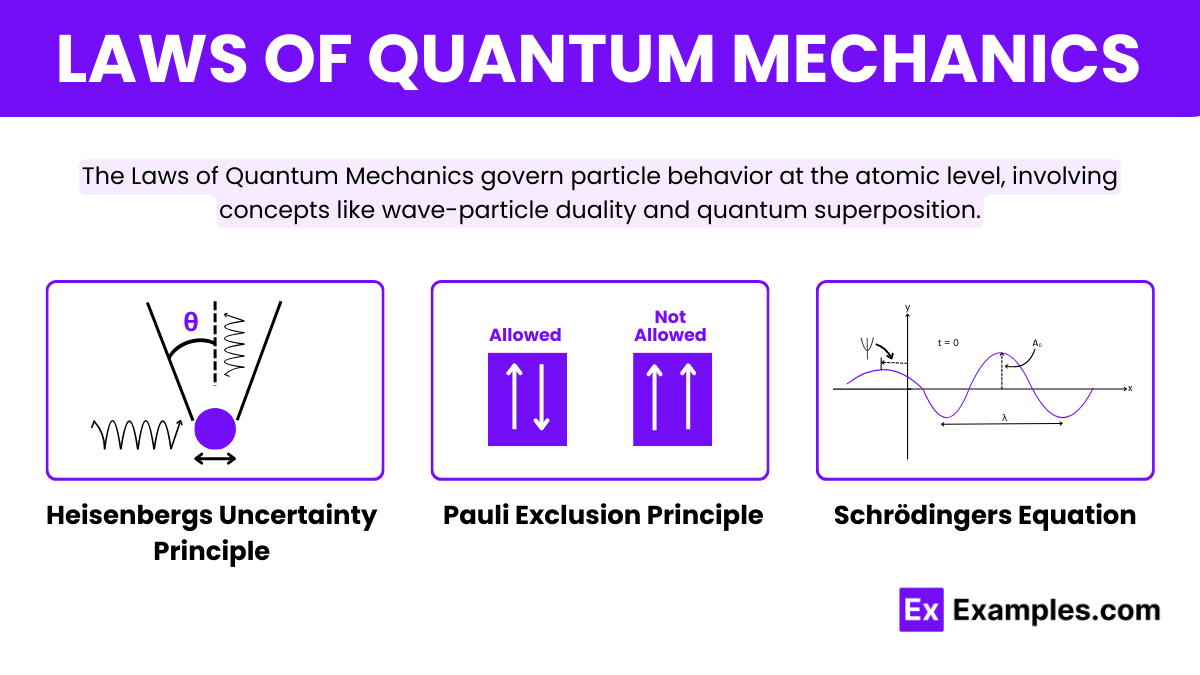
What is the Heisenberg Uncertainty Principle in quantum mechanics?
It states that particles have a fixed position and momentum.
It states that it is impossible to simultaneously know the exact position and momentum of a particle.
It states that particles do not exist in definite states.
It states that energy levels in atoms are continuous.