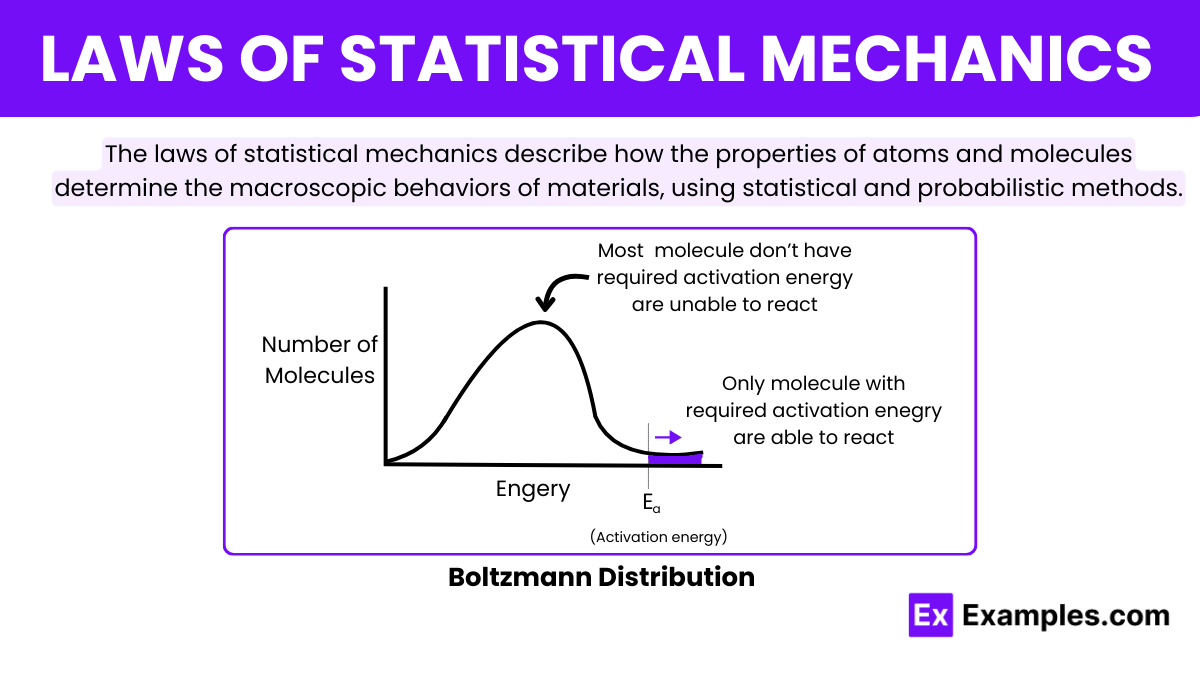
What does the equipartition theorem state in statistical mechanics?
Energy is equally distributed among all degrees of freedom
All particles have the same energy
Entropy remains constant in an isolated system
Energy can neither be created nor destroyed