Quantum Field Theory – Examples, Definition, Formula, FAQ’S

Quantum Field Theory (QFT) merges quantum mechanics with the laws of physics governing fields, portraying particles such as electrons and photons as excitations of these fields. It fundamentally transforms our understanding of matter and energy by describing interactions and transformations of particles under the framework of field dynamics. This theory is pivotal in modern physics, providing the mathematical structure to study and predict particle behavior at the quantum level, and is integral to the Standard Model of particle physics.

What Is Quantum Field Theory?

Quantum Field Theory formula

Quantum Field Theory (QFT) involves complex mathematics and multiple formulas depending on the specific interaction or particle being studied. However, a foundational formula in QFT is the Lagrangian, which is used to describe the dynamics of fields and their interactions. A general form of the QFT Lagrangian for a scalar field ϕ can be written as:

Here:

• ∂𝜇𝜙 represents the derivative of the field ϕ with respect to spacetime coordinates, indicating the field’s change over space and time.
• 𝑚m is the mass of the particle associated with the field.
• 𝑉(𝜙) is the potential energy function of the field, which can include terms for interactions with other fields or self-interactions.

This formula encapsulates how the field behaves, how it interacts with itself, and its dynamics within spacetime, providing a base from which more specific and detailed interactions can be derived in QFT.

Quantum Field Theory derivation

Deriving the foundational equations of Quantum Field Theory (QFT) is a comprehensive process that involves several steps, integrating concepts from both quantum mechanics and classical field theory. Here’s a simplified outline of the derivation process for a basic scalar field theory:

Step 1: Start with Classical Field Theory

• Lagrangian and Action: Begin with the classical field theory, defining the Lagrangian (𝐿) for a field, which is a function that describes the dynamics of the field. The action (S) is then given by the integral of the Lagrangian over spacetime: 𝑆=∫𝑑⁴𝑥 𝐿(𝜙,∂𝜇𝜙)
• Euler-Lagrange Equation: From the principle of least action, derive the Euler-Lagrange equation to obtain the field equations: ∂𝐿/∂𝜙−∂𝜇(∂𝐿/∂(∂𝜇𝜙))=0 This equation describes how the field ϕ evolves in space and time.

Step 2: Quantize the Field

• Promote Fields to Operators: In transitioning from classical to quantum fields, replace the classical fields with quantum field operators that satisfy specific commutation relations. These operators create and annihilate particles at various points in spacetime.
• Canonical Quantization: Implement canonical quantization by imposing commutation relations between the field operators and their conjugate momenta: [𝜙(𝑥),𝜋(𝑦)]=𝑖ℏ𝛿³(𝑥−𝑦) where 𝜋(𝑥) is the canonical conjugate momentum to the field 𝜙(𝑥), and 𝛿³(𝑥−𝑦) is the three-dimensional Dirac delta function.

Step 3: Introduce Interactions

• Add Interaction Terms: Modify the Lagrangian to include terms that describe interactions between fields or self-interactions. For a scalar field, this might involve terms like 𝜆𝜙⁴, which represents a self-interacting term.
• Lagrangian for Interacting Field: 𝐿=1/2(∂𝜇𝜙)²−1/2𝑚²𝜙²−𝑉(𝜙) Here, λ is the coupling constant determining the strength of the interaction.

Step 4: Solve Using Perturbation Theory

• Feynman Diagrams: For complex interactions, use perturbative techniques to approximate solutions. Feynman diagrams are graphical representations of terms in the perturbative expansion, each corresponding to a term in the series.
• Calculate Amplitudes: Compute scattering amplitudes by summing over contributions from all relevant Feynman diagrams, applying rules for vertices (interaction points) and propagators (lines representing particle exchange).

Uses of Quantum Field Theory

• Particle Physics: QFT is the framework for describing the interactions of elementary particles, including predicting the outcomes of particle collisions and the properties of the particles themselves.
• Standard Model of Particle Physics: It forms the theoretical groundwork for the Standard Model, which explains the fundamental forces (except gravity) and classifies all known subatomic particles.
• Quantum Electrodynamics (QED): As a part of QFT, QED explains how light and matter interact, providing a quantitative theory of electromagnetism that accounts for both the particle nature of photons and the wave nature of electromagnetic fields.
• Quantum Chromodynamics (QCD): QFT also includes QCD, which describes the strong interaction between quarks and gluons, the fundamental forces holding the nucleus of an atom together.
• Cosmology and Astrophysics: QFT is used to study the early universe, particularly during the inflationary epoch and for predicting phenomena such as cosmic inflation and the thermal history of the universe.
• Condensed Matter Physics: In this field, QFT techniques help understand phase transitions, superconductivity, and superfluidity by examining how macroscopic quantum systems behave.
• Computational Physics: QFT aids in developing numerical methods for simulations that are crucial in high-energy physics and condensed matter physics, where exact solutions are often unattainable.
• Technological Development: Knowledge from QFT has led to advancements in technologies such as semiconductors and laser technology, which are foundational to modern electronics and optics.

Examples for Quantum Field Theory

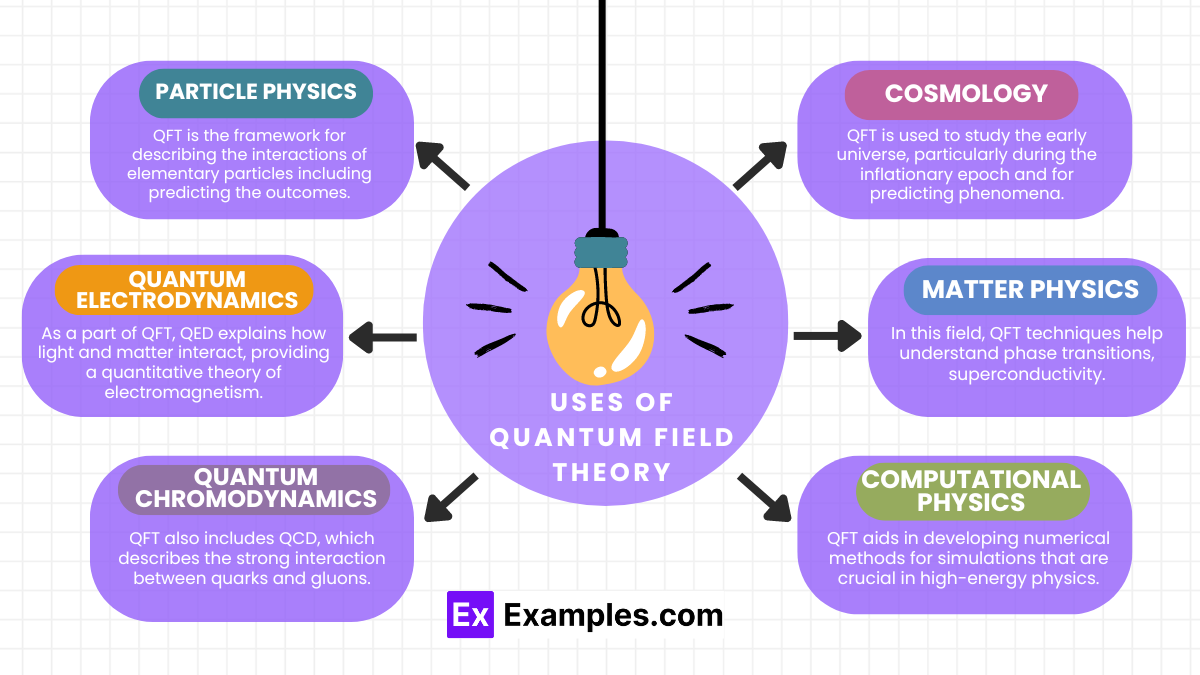
Quantum Field Theory (QFT) is a powerful tool in modern physics, underpinning many significant discoveries and technologies. Here are some practical examples illustrating its applications:

• Prediction of Particle Existence: QFT was instrumental in predicting the existence of particles like the Higgs boson before it was empirically discovered at the Large Hadron Collider (LHC) in 2012. Theoretical calculations based on QFT suggested the Higgs field and its corresponding boson, which are crucial for understanding why particles have mass.
• Quantum Electrodynamics (QED): This is a specific type of QFT that deals with the electromagnetic force, explaining interactions between light (photons) and matter (electrons). QED has been tested to extremely high precision and is used to explain phenomena such as the Lamb shift in hydrogen atoms, where electrons shift energy levels due to interactions with vacuum fluctuations.
• Quantum Chromodynamics (QCD): QCD is another facet of QFT that explains the strong force between quarks and gluons inside protons and neutrons. QCD helps scientists understand complex phenomena such as quark confinement, where quarks are permanently contained within hadrons, and the generation of most of the mass of the visible universe.
• Casimir Effect: This is a quantum phenomenon derived from QFT, where uncharged conductive plates in a vacuum attract each other due to differences in vacuum energy between the plates and outside them. This effect has practical implications in nanotechnology and materials science.
• Hawking Radiation: QFT in curved spacetime suggests that black holes emit radiation, known as Hawking radiation. This theoretical prediction, although not yet observed directly, highlights how QFT can be extended to gravitational systems and offers insights into black hole thermodynamics.
• Topological Quantum Field Theory (TQFT): Used in condensed matter physics, TQFT helps to understand and classify different states of matter, particularly topological insulators and superconductors. These materials have unique surface properties that are protected by topological invariants and are promising for applications in quantum computing.

FAQ’S

Has quantum field theory been proven?

Quantum field theory is extensively supported by experimental evidence, particularly through precise predictions matching experimental results in particle physics.

Why is quantum field theory so hard?

Quantum field theory combines advanced mathematics with complex physical concepts, challenging even experienced physicists due to its abstract nature and technical rigor.

Who are the fathers of quantum field theory?

Key contributors include Paul Dirac, Richard Feynman, and Julian Schwinger, each providing foundational insights and methodologies that shaped the development of quantum field theory.