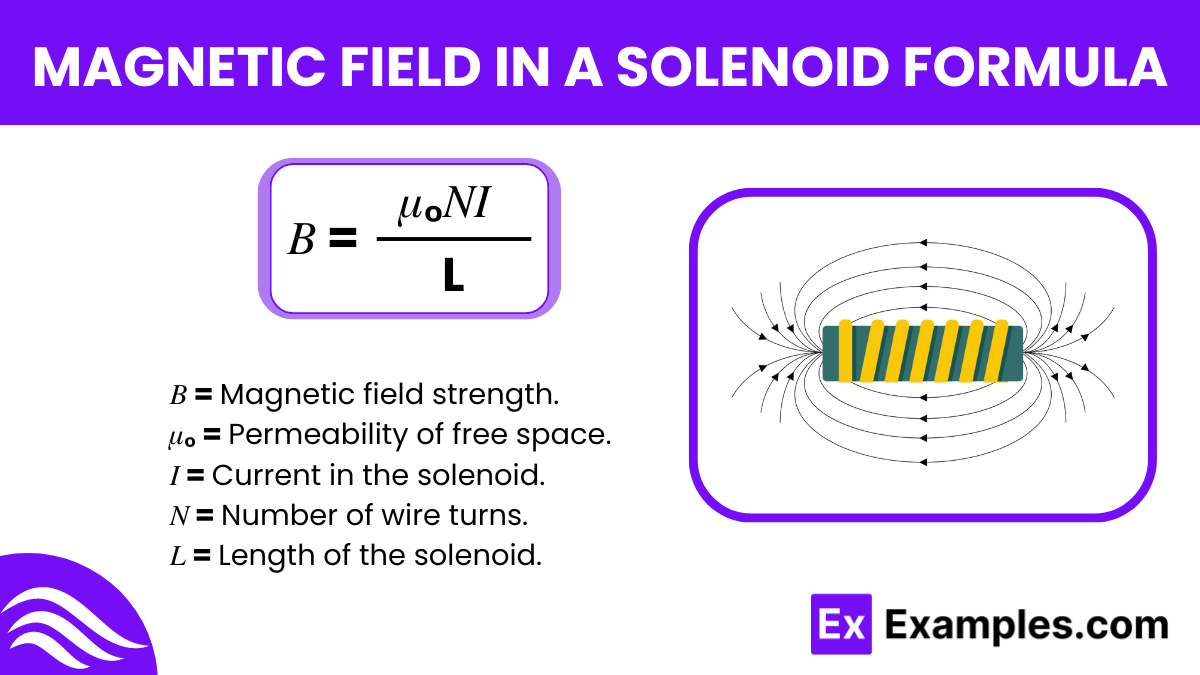
Magnetic Field In A Solenoid Formula

What is Magnetic Field In A Solenoid Formula?

The formula for the magnetic field inside a solenoid is essential in physics for calculating the field strength. The formula is represented as :

𝐵 = 𝜇ₒ𝑁𝐼 / L

𝐵 denotes the magnetic field strength.
𝜇ₒ represents the permeability of free space.
𝐼 is the current in the solenoid.
𝑁 is the number of wire turns.
𝐿 is the length of the solenoid.

This formula allows us to understand how changes in the solenoid’s current, the number of coils, or its length affect the magnetic field strength inside it. This formula was advanced by André-Marie Ampère, a pioneer in the study of electromagnetism. His research laid the groundwork for linking magnetic fields to the electric currents that generate them, culminating in the direct application of Ampère’s law.

Derivation of Magnetic Field In A Solenoid Formula

To derive the formula for the magnetic field inside a solenoid, we start with Ampère’s Law, which states:

∮ 𝐵 ⋅ 𝑑𝑙 = 𝜇ₒ𝐼ₑₙ꜀

We select a rectangular Amperian loop that runs parallel to the solenoid’s axis inside and completes the rectangle outside where the magnetic field is negligible. Here, 𝐼ₑₙ꜀ represents the total current enclosed by the loop. If 𝐼 is the current in each turn of the solenoid and there are 𝑁 turns over the length 𝐿, with 𝑛 = 𝑁 / 𝐿 being the turns per unit length, then:

𝐼ₑₙ꜀ = 𝑛𝐼𝐿

Applying Ampère’s Law, only the segment inside the solenoid contributes to the magnetic field, simplifying the integral to:

𝐵⋅𝐿=𝜇ₒ𝑛𝐼𝐿

Thus, the magnetic field 𝐵B inside the solenoid simplifies to:

𝐵=𝜇ₒ𝑛𝐼 = (𝜇ₒ𝐼𝑁) / L

Applications of Magnetic Field In A Solenoid Formula

Electromagnets: Engineers use the formula to design electromagnets used in electric motors and generators, adjusting variables to achieve desired magnetic strengths.
MRI Machines: The solenoid formula helps in designing the magnetic coils of MRI machines, crucial for creating strong and uniform magnetic fields necessary for medical imaging.
Particle Accelerators: Particle physics experiments rely on solenoids to generate magnetic fields that steer and focus particle beams.
Electric Valves: Solenoids actuate electric valves in fluid systems, controlling the flow based on the magnetic field strength derived from the formula.
Telecommunication Devices: The formula assists in designing solenoids for telecommunication devices, where magnetic fields play a role in signal processing and relay mechanisms.

Example Problems of Magnetic Field In A Solenoid Formula

Problem 1: Basic Calculation

Question: A solenoid has a length of 50 cm, contains 200 turns, and a current of 2 A flows through it. Calculate the magnetic field inside the solenoid. Assume the permeability of free space, 𝜇ₒ, is 4𝜋×10⁻⁷ 𝑇⋅𝑚/𝐴.

Solution:

Convert length from cm to meters: 𝐿=0.50 𝑚

Use the formula 𝐵 = 𝜇ₒ𝐼𝑁 / 𝐿

Substitute the values:

𝐵 = ( (4𝜋×10⁻⁷ 𝑇⋅𝑚/𝐴)(2 𝐴)(200) ) / 0.50 𝑚= ( 502.654 × 10⁻⁴ 𝑇) / 0.50 𝑚

Calculate:𝐵=0.2007 𝑇

Answer: The magnetic field inside the solenoid is 0.2007 𝑇.

Problem 2: Effects of Changing Current

Question: Using the same solenoid from Problem 1, what would the magnetic field be if the current is increased to 5 A?

Solution:

Use the same length, number of turns, and 𝜇ₒ from Problem 1.

Substitute the new current into the formula:

𝐵 = ( (4𝜋 × 10⁻⁷ 𝑇⋅𝑚/𝐴) (5 𝐴) (200) ) / 0.50 𝑚= ( 1256.637 × 10⁻⁴ 𝑇) / 0.50 𝑚

Calculate:𝐵=0.5027 𝑇

Answer: The Magnetic field is now 0.5027 𝑇.

Problem 3: Impact of Changing the Number of Turns

Question: If the number of turns in the solenoid from Problem 1 is increased to 400 turns while keeping the current at 2 A, what is the new magnetic field?

Solution:

Keep the length and 𝜇ₒ constant.

Substitute the new number of turns into the formula:

𝐵 = ( (4𝜋 × 10⁻⁷ 𝑇⋅𝑚/𝐴) (2 𝐴) (400) ) / 0.50 𝑚 = (1005.31 × 10⁻⁴ 𝑇) /0.50 𝑚

Answer: The Magnetic field inside the solenoid is 0.4011 𝑇.

FAQs

What is the Magnetic Field Rule of a Solenoid?

The Magnetic field inside a solenoid is uniform and parallel to its axis, following the right-hand rule for current direction.

What is the Formula for the Magnetic Moment of a Solenoid?

The Magnetic moment (𝜇) of a solenoid is calculated by 𝜇=𝑁𝐼𝐴, where 𝑁 is turns, 𝐼 is current, and 𝐴 is area.

What is the Rule for the Magnetic Field of a Coil?

A coil’s Magnetic field circles the wire, determined by the right-hand rule, where thumb direction indicates current and fingers show field lines.

Magnetic Field In A Solenoid Formula