Radian
Radian
What is Radian?
A radian is a unit of angular measurement used in mathematics and physics.A radian is a measure of angle created when the arc length of a circle equals the radius. Essentially, it’s how we measure the bend of a circle using the radius as a guide. One complete circle is about 6.28 radians, equivalent to 360 degrees.
Formula :
Additional Formulas Involving Radian
Arc Length:
Where L is the arc length, r is the radius of the circle, and θ is the angle in radians.
Area of a Sector:
Where A is the area, r is the radius of the circle, and θ is the angle in radians.
Angular Velocity:
Where ω is the angular velocity, θ is the angular displacement in radians, and t is the time.
SI Multiples of Radian
While the radian is a fundamental unit of angular measurement, it doesn’t typically use SI (International System of Units) prefixes like kilo, mega, etc. However, theoretically, they could be applied:
| SI Prefix | Unit Name | Multiple | Equivalent in Radians | Description |
|---|---|---|---|---|
| Kiloradian | Kiloradian (krad) | 10³ | 1 kiloradian = 1,000 radians | Used for larger angular measurements, not commonly employed. |
| Milliradian | Milliradian (mrad) | 10−³ | 1 milliradian = 0.001 radians | Provides finer precision for detailed measurements. |
Conversion of Radian into other Units
| To Unit | Conversion Factor | Conversion from 10 radians |
|---|---|---|
| Degrees (°) | 1 radian = 57.2958 degrees | 572.958 degrees |
| Gradians (gon) | 1 radian = 63.6620 gradians | 636.620 gradians |
| Minutes of arc | 1 radian = 3437.75 arc minutes | 34377.5 arc minutes |
| Seconds of arc | 1 radian = 206265 arc seconds | 2062650 arc seconds |
| Milliradians (mrad) | 1 radian = 1000 milliradians | 10,000 milliradians |
| Microradians (µrad) | 1 radian = 1,000,000 microradians | 10,000,000 microradians |
Converting radians into other units of angular measurement is a common task in mathematics, physics, and engineering. Here are the key conversion formulas:
From Radians to Degrees:
This formula converts radians to degrees by multiplying the radian measure by 180/π Since 180° is equivalent to π radians.
From Radians to Gradians (gon):
From Radians to Minutes of Arc:
Since each degree contains 60 minutes of arc, this formula converts radians to minutes of arc by first converting radians to degrees and then multiplying by 60.
From Radians to Seconds of Arc:
Similar to the conversion to minutes of arc, this formula first converts radians to degrees and then multiplies by 3600 to obtain seconds of arc.
These conversions allow you to express angles in radians in terms of degrees, minutes of arc, or seconds of arc, depending on the desired level of precision.
From Radians to Milliradians (mrad)
From Radians to Microradians (µrad)
Difference Between Radian And Milliradian
This table succinctly outlines the distinctions between radians and milliradians, including their magnitudes, approximate conversions, and typical applications.
| Characteristic | Radian (rad) | Milliradian (mrad) |
|---|---|---|
| Magnitude | A unit of angular measurement where one radian subtends an arc length equal to the radius of the circle. | One milliradian is equal to one-thousandth of a radian. |
| Approximate Conversion | 1 rad = 57.296 degrees | 1 rad = 1,000 milliradians |
| Typical Applications | Mathematical and scientific contexts, calculus, physics, engineering. | Ballistics, firearm optics, surveying, where precise angular measurements are required. |
Uses of Radian
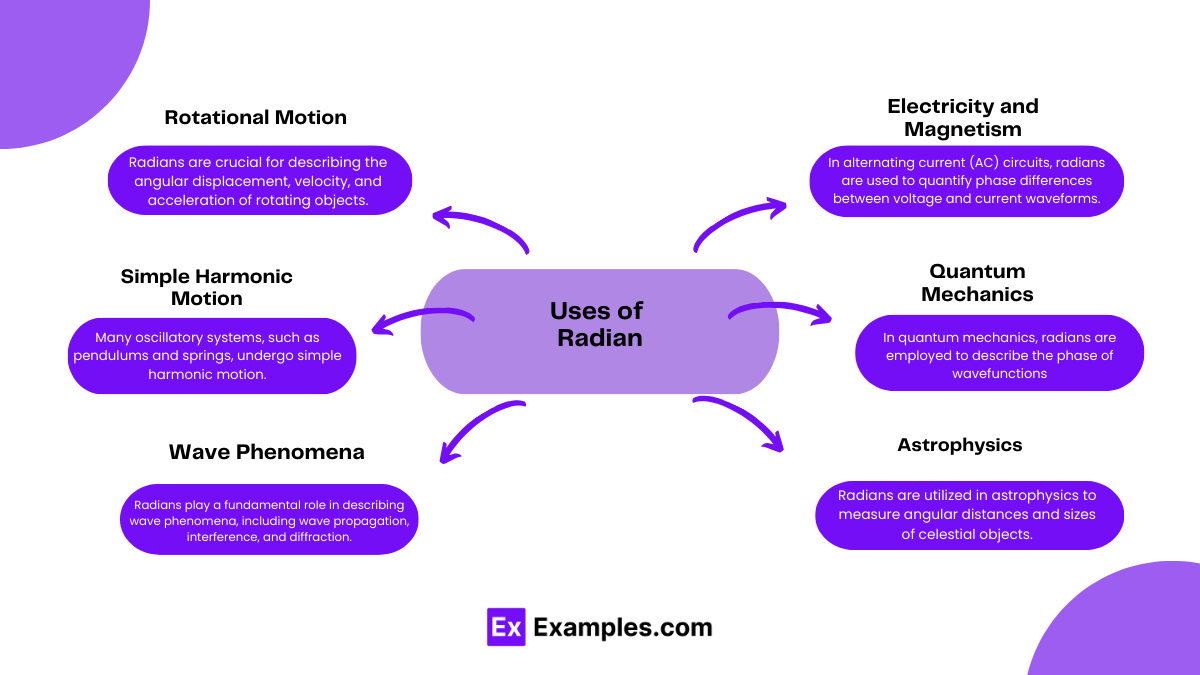
Radians are extensively used in various branches of physics due to their natural relationship with circular motion and angles. Some key applications include:
1. Rotational Motion: Radians are crucial for describing the angular displacement, velocity, and acceleration of rotating objects. In mechanics, rotational kinematics and dynamics equations are often formulated in terms of radians to represent the angle of rotation.
2.Simple Harmonic Motion: Many oscillatory systems, such as pendulums and springs, undergo simple harmonic motion. Radians are employed to measure the phase angle and angular frequency of these oscillations, facilitating the analysis and prediction of their behavior.
3.Wave Phenomena: Radians play a fundamental role in describing wave phenomena, including wave propagation, interference, and diffraction. Angular measures are utilized to express phase differences between waveforms and to calculate wave parameters like wavelength and wave vector.
4.Electricity and Magnetism: In alternating current (AC) circuits, radians are used to quantify phase differences between voltage and current waveforms. Phasors, which represent sinusoidal quantities, are often expressed in radians to simplify calculations in circuit analysis.
5.Quantum Mechanics: In quantum mechanics, radians are employed to describe the phase of wavefunctions, which represent the probability amplitudes of particles. The phase angle plays a crucial role in determining interference patterns and probability distributions in quantum systems.
6.Astrophysics:Radians are utilized in astrophysics to measure angular distances and sizes of celestial objects, such as stars, galaxies, and planetary orbits. Angular measures are essential for determining positions, motions, and dimensions in the vastness of the universe.
FAQ’S
Why do we use radians instead of degrees in calculus and physics?
Radians are preferred in calculus and physics because they simplify many mathematical formulas and relationships.
How do radians relate to circular motion?
In circular motion, radians are used to measure angles as objects rotate around a center point. The angle in radians represents the fraction of the circle that has been traversed by the rotating object.
Share :
