Avogadro’s Hypothesis and Number – Examples, Definition, Derivation, Uses, Limitations

Avogadro’s Hypothesis and Number play a crucial role in both chemistry and physics by providing a fundamental understanding of how gases behave under various conditions. Avogadro’s Hypothesis states that equal volumes of gases, at the same temperature and pressure, contain an equal number of molecules. This principle laid the groundwork for Avogadro’s Number, which defines the number of particles in one mole of a substance as 6.022×10²³. This concept bridges the gap between the microscopic world of atoms and molecules and the macroscopic world we observe, helping scientists apply the laws of physics to chemical reactions and processes.

What is Avogadro’s Hypothesis?

What is Avogadro’s Number?

Avogadro’s Hypothesis Formula

The mathematical expression of Avogadro’s Hypothesis is:

Where:

• V is the volume of the gas.
• n is the number of moles of the gas.

Alternative Expression

Avogadro’s Law can also be written as:

Where:

• 𝑉₁​ and 𝑉₂​ are the volumes of gas samples 1 and 2.
• 𝑛₁​ and 𝑛₂ are the number of moles of gas samples 1 and 2.

Avogadro’s Number Formula

he formula involving Avogadro’s Number relates the number of particles (N) to the amount of substance in moles (n). It is expressed as

• 𝑁 is the total number of particle
• 𝑛 is the number of moles
• 𝑁𝐴​ is Avogadro’s Number (6.022×10²³ particles per mole).

This formula allows scientists to convert between the macroscopic scale of moles and the microscopic scale of individual particles, providing a fundamental tool in chemistry for quantifying substances.

Graphical Representation of Avogadro’s Hypothesis

At constant pressure and temperature, Avogadro’s hypothesis can be expressed via the following formula:

𝑉 ∝ 𝑛

𝑉/𝑛=𝑘

Where 𝑉 is the volume of the gas, 𝑛 denotes the amount of gaseous substance (often expressed in moles), and 𝑘 is a constant. When the amount of gaseous substance is increased, the corresponding increase in the volume occupied by the gas can be calculated with the help of the following formula:

𝑉₁/𝑛₁ = 𝑉₂/𝑛₂ (=𝑘, as per Avogadro’s hypothesis)

The graphical representation of Avogadro’s hypothesis (with the amount of substance on the X-axis and volume on the Y-axis) is illustrated below:

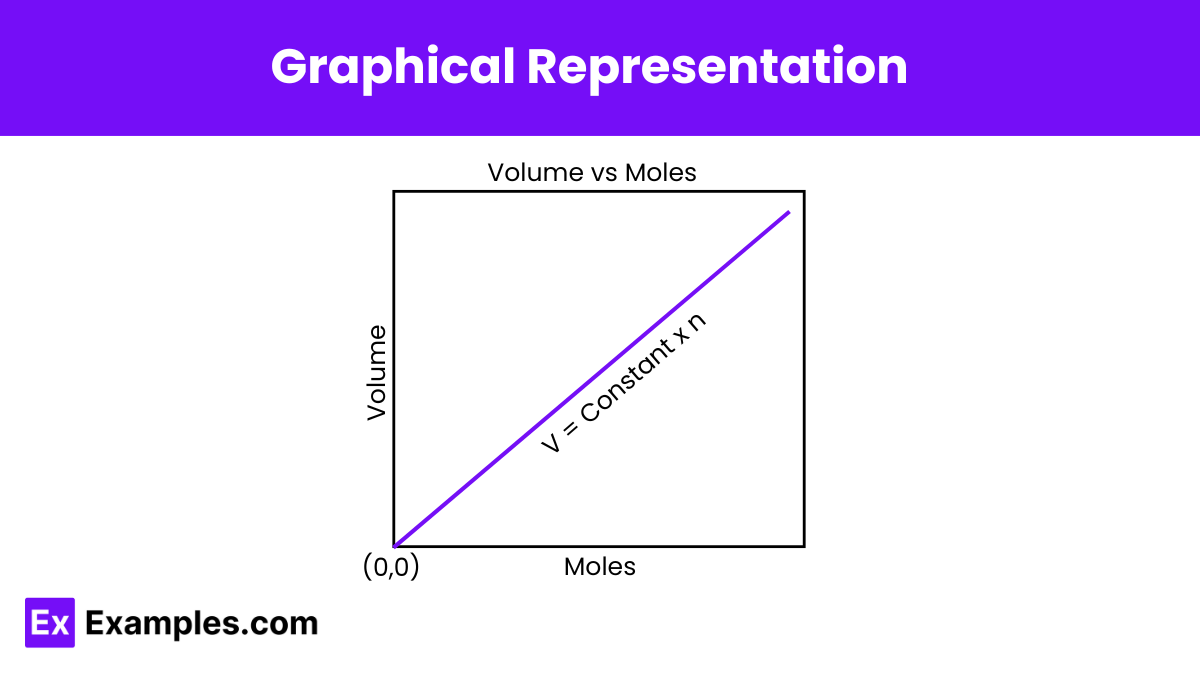
Here, the straight line (which indicates that the two quantities are directly proportional) passes through the origin, implying that zero moles of gas will occupy zero volume.

Derivation of Avogadro’s Hypothesis

Step 1: Understand the Ideal Gas Law

The Ideal Gas Law is:

𝑃𝑉 = 𝑛𝑅𝑇

Where:

• 𝑃 is the pressure of the gas.
• 𝑉 is the volume of the gas.
• 𝑛 is the number of moles of the gas.
• 𝑅 is the universal gas constant.
• 𝑇 is the temperature of the gas.

Step 2: Isolate the Volume

To explore the relationship between volume (𝑉) and the number of moles (𝑛), we rearrange the Ideal Gas Law:

𝑉=𝑛𝑅𝑇/𝑃​

Step 3: Hold Temperature and Pressure Constant

Assume that the temperature (𝑇) and pressure (𝑃) are constant. Under these conditions, the equation simplifies to:

𝑉 ∝ 𝑛

This means that the volume (𝑉) is directly proportional to the number of moles (𝑛) of the gas when temperature and pressure are constant.

Step 4: Interpret the Proportionality

Since 𝑉 ∝ 𝑛, if you have equal volumes of two different gases at the same temperature and pressure, they must contain the same number of moles of gas.

Step 5: Link Moles to Molecules

One mole of any gas contains Avogadro’s number (𝑁ₐ​) of molecules, where:

𝑁𝐴 ≈ 6.022×10²³ molecules/mol

Step 6: Apply to Different Gases

Therefore, if equal volumes of different gases contain the same number of moles under the same conditions of temperature and pressure, they also contain the same number of molecules.

How was Avogadro’s Number Determined or Derived?

Avogadro’s Number was determined through various experimental methods and theoretical calculations, providing a way to quantify the number of particles in a mole. Here is a simplified explanation of the process:

1. Historical Context: The concept of the mole and Avogadro’s Number emerged from the work of early chemists like Amedeo Avogadro, who hypothesized that equal volumes of gases at the same temperature and pressure contain an equal number of molecules.
2. Electrolysis Method: One of the first experimental methods involved electrolysis. By measuring the amount of gas produced at the electrodes during electrolysis, scientists could calculate the number of atoms or molecules involved. The charge of one mole of electrons (Faraday’s constant) was used in conjunction with the total charge passed to determine the number of particles.
3. X-ray Crystallography: This technique involves measuring the density of atoms in a crystal lattice. By determining the crystal structure and the spacing between atoms, scientists could calculate the number of atoms in a known volume. This allowed them to estimate the number of atoms in a mole of the substance.
4. Brownian Motion: Albert Einstein and Jean Perrin contributed significantly to the determination of Avogadro’s Number through the study of Brownian motion. Einstein’s theoretical work on the random motion of particles in a fluid and Perrin’s experimental observations provided a way to calculate the number of molecules in a given volume of gas.
5. Gas Laws and Molecular Weights: Using the ideal gas law (PV = nRT) and precise measurements of gas properties, scientists could relate the volume of a gas to the number of molecules. Determining the molar volume of gases at standard temperature and pressure (STP) and the mass of a known volume of gas allowed for the calculation of the number of molecules.
6. Modern Methods: Advanced techniques like mass spectrometry and more refined X-ray diffraction methods continue to provide precise measurements of atomic and molecular structures, further confirming Avogadro’s Number.

By combining these experimental and theoretical approaches, scientists established Avogadro’s Number as 6.022×10²³, providing a fundamental constant that bridges the microscopic world of atoms and molecules with the macroscopic world of grams and liters.

Uses of Avogadro’s Hypothesis

• Understanding Gas Behavior: Avogadro’s Hypothesis helps us understand the behavior of gases. By stating that equal volumes of gases, at the same temperature and pressure, contain an equal number of molecules, it allows scientists to predict how gases will react under different conditions.
• Ideal Gas Law: Avogadro’s Hypothesis is a key component of the Ideal Gas Law, 𝑃𝑉=𝑛𝑅𝑇. This law is fundamental in chemistry and physics for calculating the properties of gases. It helps in determining the relationships between pressure, volume, temperature, and the number of moles of a gas.
• Determining Molecular Weights: The hypothesis allows chemists to determine the molecular weights of gases. By comparing the weights of equal volumes of different gases, they can infer the relative weights of molecules.
• Stoichiometry of Gaseous Reactions: Avogadro’s Hypothesis is crucial in the stoichiometry of reactions involving gases. It helps in predicting the volumes of gases consumed and produced in chemical reactions, making it easier to balance chemical equations.
• Standard Temperature and Pressure (STP) Calculations: At STP (0°C and 1 atm pressure), one mole of any ideal gas occupies 22.4 liters. This concept, derived from Avogadro’s Hypothesis, is used in various calculations in chemistry to relate the volume of gas to the amount in moles.
• Gas Densities and Molar Volumes: By using Avogadro’s Hypothesis, scientists can calculate the densities and molar volumes of gases. This is important in fields like material science and engineering where understanding gas properties is crucial.

Uses of Avogadro’s Number

• Determine Moles: Avogadro’s Number converts the number of particles to moles for chemical calculations.
• Calculate Atomic Mass: It helps relate atomic and molecular masses to grams.
• Stoichiometry: Avogadro’s Number enables precise stoichiometric calculations in chemical reactions.
• Gas Laws: It is used to apply the Ideal Gas Law, relating volume, temperature, and pressure to the number of moles.
• Avogadro’s Law: The number is essential for understanding the relationship between gas volume and the number of molecules.
• Molecular Count: Avogadro’s Number determines the number of molecules or atoms in a given mass of substance.
• Chemical Equilibrium: It assists in calculating concentrations and quantities in equilibrium reactions.
• Solutions and Concentrations: Avogadro’s Number helps calculate molarity and other concentration units.
• Biochemical Applications: It is used in determining the number of molecules in biological samples, such as DNA or proteins.
• Material Science: The number aids in quantifying atoms or molecules in a given volume of material.

Limitations of Avogadro’s Law

• Ideal Gas Assumption :Avogadro’s Law assumes that gases behave ideally. Real gases deviate from ideal behavior, especially under high pressure and low temperature. In these conditions, the interactions between gas molecules and the volume occupied by the gas molecules themselves become significant, causing deviations from Avogadro’s Law.
• Non-Ideal Gas Behavior:
• High Pressure: At high pressures, gas molecules are forced closer together, and the volume occupied by the gas molecules themselves becomes significant compared to the volume of the container.
• Low Temperature: At low temperatures, gas molecules have lower kinetic energy, and intermolecular attractions become significant, leading to deviations from ideal gas behavior.
• Nature of Gas: Different gases have different intermolecular forces, which can cause deviations from Avogadro’s Law. For example:
• Polar Gases: Gases with strong intermolecular forces (e.g., water vapor) deviate more from ideal behavior compared to non-polar gases (e.g., helium).
• Large Molecules: Larger gas molecules occupy more space and have more significant intermolecular interactions, causing greater deviations.
• Real Gas Equations: To account for these deviations, real gas behavior is often described using the Van der Waals equation or other equations of state that include correction factors for intermolecular forces and molecular volume. These equations provide more accurate predictions for the behavior of real gases under various conditions.
• Limitation to Gaseous State: Avogadro’s Law applies strictly to gases and not to liquids or solids. The behavior of molecules in liquids and solids is governed by different principles due to the significant intermolecular forces present in these states of matter.

Limitations of Avogadro’s Number

1. Applicability to Ideal Conditions: Avogadro’s Number assumes ideal conditions, which may not accurately represent real-world scenarios where gases deviate from ideal behavior.
2. Measurement Precision: Determining Avogadro’s Number with absolute precision is challenging due to limitations in experimental techniques and measurement accuracy.
3. Macroscopic Scale: While useful for large-scale calculations, Avogadro’s Number may not be practical for understanding interactions at the individual particle level.
4. Complex Calculations: Using Avogadro’s Number in complex chemical reactions and processes can be cumbersome and may require advanced computational tools.
5. Variability in Substances: Avogadro’s Number applies universally, but variations in molecular size, shape, and interactions can complicate its direct application in certain contexts.

Examples for Avogadro’s Hypothesis

1. Understanding Gas Behavior: Avogadro’s Hypothesis helps predict how gases behave under different conditions. For instance, it explains why equal volumes of hydrogen and oxygen gases, at the same temperature and pressure, contain the same number of molecules, which is crucial for understanding gas reactions.
2. Ideal Gas Law: Avogadro’s Hypothesis is a key component of the Ideal Gas Law, which is used to calculate properties of gases in various scientific and industrial processes. For example, it helps determine how much gas will be produced or consumed in a chemical reaction.
3. Molecular Weight Determination: Chemists use Avogadro’s Hypothesis to determine the molecular weights of gases. By comparing the weights of equal volumes of different gases, scientists can infer their molecular weights, aiding in the identification of unknown gases.
4. Stoichiometry of Gaseous Reactions: Avogadro’s Hypothesis is essential for balancing chemical equations involving gases. It allows chemists to predict the volumes of reactants and products in gas reactions, which is vital for laboratory and industrial chemical synthesis.
5. Standard Temperature and Pressure Calculations: At standard temperature and pressure (STP), one mole of any ideal gas occupies 22.4 liters. This concept, derived from Avogadro’s Hypothesis, is used to relate the volume of a gas to the amount in moles in various scientific calculations.
6. Gas Density and Molar Volume: Avogadro’s Hypothesis helps calculate the density and molar volume of gases, which is important for applications in material science and engineering. For instance, it aids in designing gas storage containers and understanding the behavior of gases in different environments.
7. Biological Respiration: Avogadro’s Hypothesis explains the exchange of gases in human lungs. It shows how equal volumes of inhaled and exhaled air contain the same number of molecules, helping in the study of respiratory physiology and medical treatments for lung conditions.

Examples of Avogadro’s Number

1. Water Molecules: One mole of water (18 grams) contains 6.022×10²³ water molecules.
2. Carbon Atoms: One mole of carbon-12 (12 grams) has 6.022×10²³ carbon atoms.
3. Oxygen Molecules: One mole of oxygen gas (32 grams) includes 6.022×10²³ oxygen molecules.
4. Hydrogen Atoms: One mole of hydrogen gas (2 grams) consists of 6.022×10²³ hydrogen atoms.
5. Sodium Chloride: One mole of table salt (58.44 grams) contains 6.022×10²³ formula units of NaCl.
6. Avogadro’s Constant: One mole of any element, like gold (197 grams), has 6.022×10²³ gold atoms.
7. Molecular Count: In 1 mole of glucose (180 grams), there are 6.022×10²³ glucose molecules.
8. Gas Molecules: At STP, one mole of any gas occupies 22.4 liters and contains 6.022×10²³ molecules.
9. Electron Count: One mole of electrons has 6.022×10²³ electrons.
10. DNA Molecules: One mole of a specific DNA sequence contains 6.022×10²³ DNA molecules.

FAQ’s