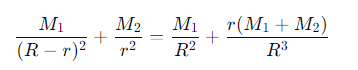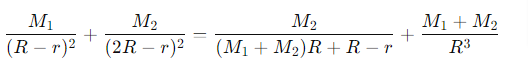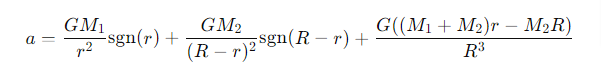What is a Lagrangian point in a two-body system?
A location where the gravitational forces cancel each other out
A point where the two bodies have equal masses
A point where the orbital period of the bodies is equal
A position where an object experiences no net force