Area and Volume
Understanding the concepts of area and volume is crucial for solving various geometry and real-world problems, which are frequently encountered on the Digital SAT Exam. Area refers to the amount of space inside a two-dimensional shape, while volume measures the space a three-dimensional object occupies. Mastery of these concepts involves knowing the formulas for different shapes and solids and being able to apply them to solve problems.
Learning Objectives
In this section, you will learn to calculate the area of various two-dimensional shapes, such as rectangles, triangles, and circles, as well as the volume of three-dimensional solids, including cubes, cylinders, and spheres. You will also learn to apply these formulas to solve real-world problems and understand the principles behind these calculations. By the end of this section, you will be able to accurately compute area and volume and tackle related questions on the Digital SAT Exam.
Area
For mastering area, learn formulas and applications for rectangles, triangles, circles, parallelograms, and trapezoids. Practice calculating the area of these various shapes and solving real-world geometry problems.
Rectangle
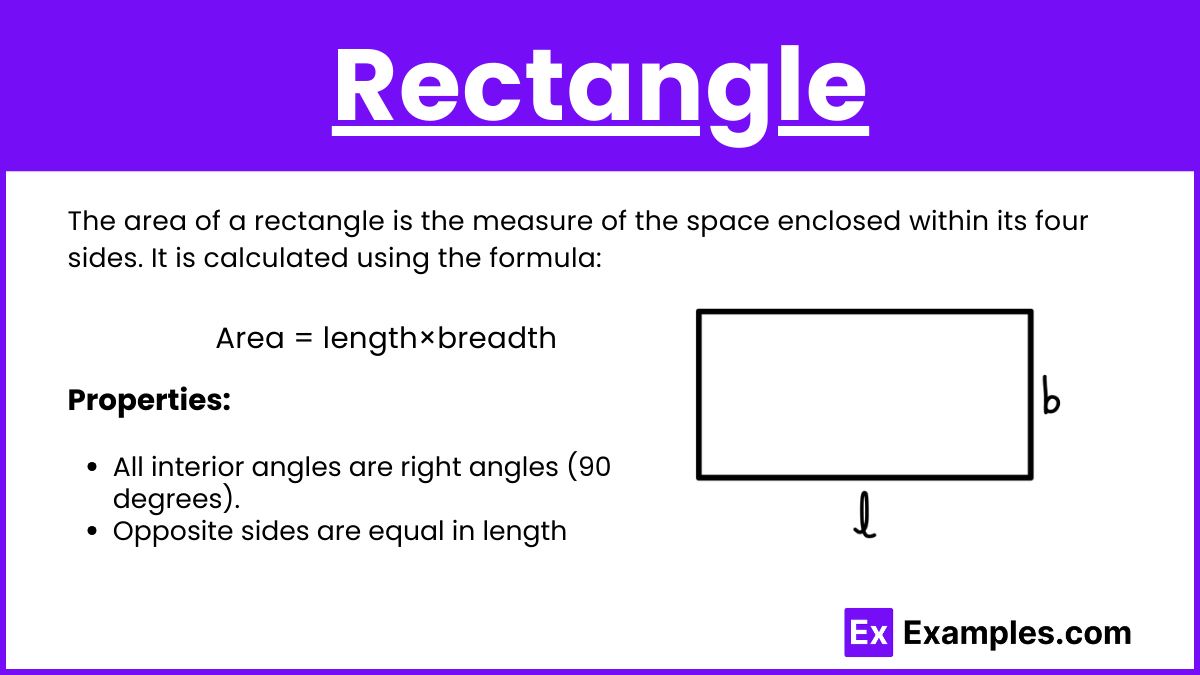
The area of a rectangle is the measure of the space enclosed within its four sides. It is calculated using the formula:
Area = length×breadth
For a rectangle with length l and breadth b:
Area = l×b
Properties:
- All interior angles are right angles (90 degrees).
- Opposite sides are equal in length.
Triangle
The area of a triangle is determined by its base and height. The formula for the area of a triangle is:
\( \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \)
For a triangle with base b and height h:
\( \text{Area} = \frac{1}{2} \times \text{b} \times \text{h} \)
Types of Triangles:
- Equilateral Triangle: All sides and angles are equal.
- Isosceles Triangle: Two sides and two angles are equal.
- Scalene Triangle: All sides and angles are different.
Circle
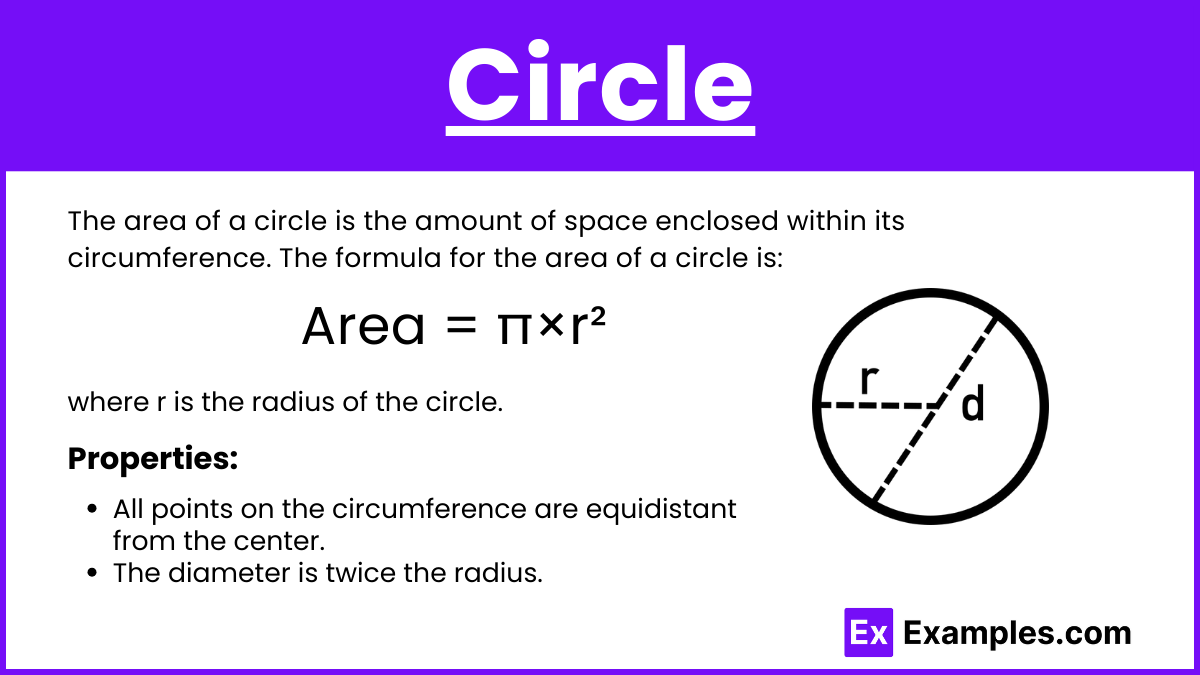
The area of a circle is the amount of space enclosed within its circumference. The formula for the area of a circle is:
Area = π×r²
where r is the radius of the circle.
Properties:
- All points on the circumference are equidistant from the center.
- The diameter is twice the radius.
Parallelogram
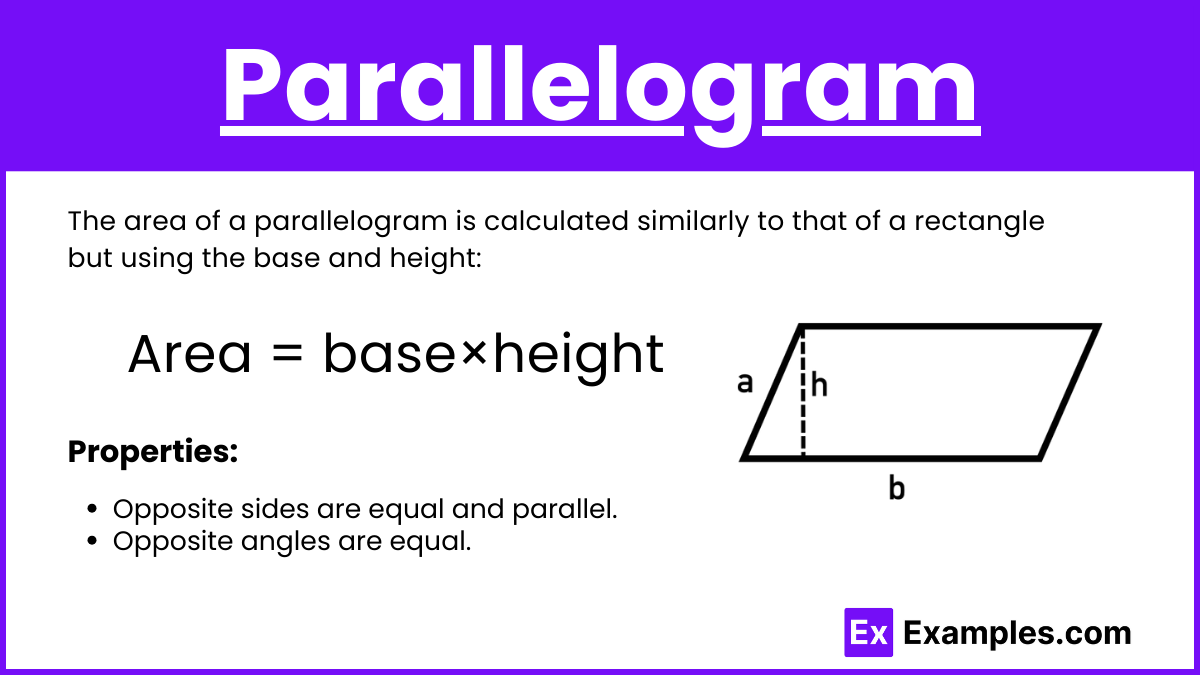
The area of a parallelogram is calculated similarly to that of a rectangle but using the base and height:
Area = base×height
For a parallelogram with base b and height h:
Area = b×h
Properties:
- Opposite sides are equal and parallel.
- Opposite angles are equal.
Volume
For mastering volume, learn formulas and applications for cubes, rectangular prisms, cylinders, spheres, and cones. Practice calculating the volume of these various solids and solving real-world geometry problems.
Cube
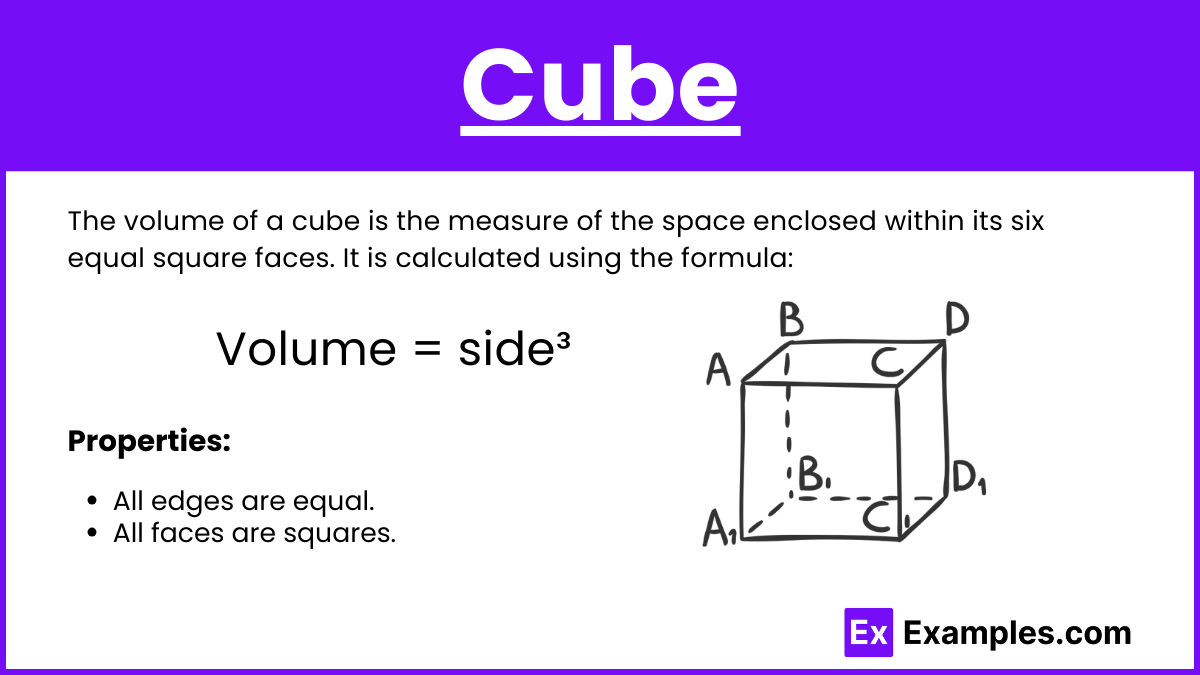
The volume of a cube is the measure of the space enclosed within its six equal square faces. It is calculated using the formula:
Volume = side³
For a cube with side length s:
Volume = s³
Properties:
- All edges are equal.
- All faces are squares.
Rectangular Prism
The volume of a rectangular prism, also known as a cuboid, is calculated by multiplying its length, width, and height:
Volume = length×width×height
For a prism with length l, width w, and height h:
Volume = l×w×h
Properties:
- Opposite faces are rectangles of equal area.
- Edges meeting at a vertex are perpendicular to each other.
Cylinder
The volume of a cylinder is found by multiplying the area of its circular base by its height:
Volume = π×r²×h
where r is the radius of the base and h is the height of the cylinder.
Properties:
- The bases are parallel and congruent circles.
- The height is the perpendicular distance between the bases.
Sphere
The volume of a sphere is calculated using the formula:
\( \text{Volume} = \frac{4}{3} \times \pi \times r^3 \)
where r is the radius of the sphere.
Properties:
- All points on the surface are equidistant from the center.
- It has no edges or vertices.
Cone
The volume of a cone is determined by using one-third the area of its base times its height:
\( \text{Volume} = \frac{1}{3} \times \pi \times r^2 \times h \)
where r is the radius of the base and h is the height of the cone.
Properties:
- The base is a circle.
- The height is the perpendicular distance from the base to the apex.
Examples of Area and Volume
Example 1: Area of a Rectangle
Calculate the area of a rectangle with a length of 8 cm and a width of 5 cm.
Area = 8×5 = 40cm²
Example 2: Area of a Triangle
Find the area of a triangle with a base of 10 cm and a height of 6 cm.
\( \text{Area} = \frac{1}{2} \times 10 \times 6 = 30 \, \text{cm}^2 \)
Example 3: Area of a Circle
Determine the area of a circle with a radius of 7 cm.
Area = π×7² = 49π ≈ 153.94cm²
Example 4: Volume of a Cube
Calculate the volume of a cube with a side length of 4 cm.
Volume = 4³ = 64cm³
Example 5: Volume of a Cylinder
Find the volume of a cylinder with a radius of 3 cm and a height of 10 cm.
Volume = π×3²×10 = 90π ≈ 282.74cm³
Practice Questions
Question 1
What is the area of a triangle with a base of 12 cm and a height of 8 cm?
A) 48 cm²
B) 72 cm²
C) 96 cm²
D) 100 cm²
Answer: A
Explanation: The area of a triangle is calculated using the formula \( \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \).
\( \text{Area} = \frac{1}{2} \times 12 \times 8 = 48 \, \text{cm}^2 \)
Question 2
A cylinder has a radius of 5 cm and a height of 12 cm. What is its volume?
A) 300π cm³
B) 60π cm³
C) 150π cm³
D) 100π cm³
Answer: A
Explanation: The volume of a cylinder is given by the formula Volume = π×r²×h
Volume = π×5²×12 = 300πcm³
Question 3
Find the volume of a sphere with a radius of 6 cm.
A) 864π cm³
B) 144π cm³
C) 216π cm³
D) 288π cm³
Answer: D
Explanation: The volume of a sphere is given by the formula \( \text{Volume} = \frac{4}{3} \times \pi \times r^3 \).
\( \text{Volume} = \frac{4}{3} \times \pi \times 6^3 = \frac{4}{3} \times \pi \times 216 = 288\pi \, \text{cm}^3 \)