Right Triangles and Trigonometry

Last Updated: September 25, 2024

Notes

Right triangles and trigonometry are fundamental concepts in geometry and are frequently tested on the Digital SAT Exam. A right triangle is a type of triangle that has one angle measuring exactly 90 degrees. Trigonometry is the branch of mathematics that deals with the relationships between the sides and angles of triangles, particularly right triangles. Understanding these concepts is crucial for solving a variety of geometric problems and real-world applications.

Learning Objectives

In this section, you will learn to identify and analyze right triangles, understand the Pythagorean theorem, and apply trigonometric ratios to solve problems involving right triangles. You will also learn to use the unit circle and solve trigonometric equations. By the end of this section, you will be able to confidently handle right triangles and trigonometry problems on the Digital SAT Exam.

Right Triangles

A right triangle has one angle equal to 90 degrees. The side opposite the right angle is called the hypotenuse, and it is the longest side of the triangle. The other two sides are called the legs. The basic properties and theorems related to right triangles include:

Pythagorean Theorem

The Pythagorean theorem is a fundamental principle in geometry. It states that in a right triangle, the square of the length of the hypotenuse (c) is equal to the sum of the squares of the lengths of the other two sides (a and b):

a²+b²=c²

Special Right Triangles

There are two special types of right triangles that often appear in problems:

45°-45°-90° Triangle: In this triangle, the legs are congruent, and the hypotenuse is 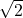$\sqrt{2}$ times the length of each leg. If the length of each leg is x, then the hypotenuse is $x\sqrt{2}$ .
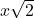30°-60°-90° Triangle: In this triangle, the hypotenuse is twice the length of the shorter leg, and the longer leg is 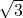$\sqrt{3}$ times the length of the shorter leg. If the shorter leg has length x, then the longer leg is 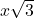$x\sqrt{3}$ and the hypotenuse is 2x.

Trigonometric Ratios

Trigonometric ratios relate the angles of a right triangle to the lengths of its sides. The primary trigonometric ratios are sine, cosine, and tangent, abbreviated as sin, cos, and tan, respectively.

Definitions

For a right triangle with an angle (\theta):

Sine (sin): $\sin \theta = \frac{\text{opposite}}{\text{hypotenuse}}$
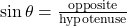
Cosine (cos): $\cos \theta = \frac{\text{adjacent}}{\text{hypotenuse}}$
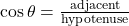
Tangent (tan): $\tan \theta = \frac{\text{opposite}}{\text{adjacent}}$

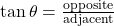
Inverse Trigonometric Functions

Inverse trigonometric functions allow you to find the angles when the sides of the triangle are known:

Arcsine 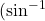$(\sin^{-1}$ or $\text{asin})$
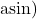
Arccosine 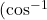$(\cos^{-1}$ or $\text{acos})$
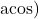
Arctangent 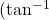$(\tan^{-1}$ or $\text{atan})$

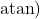
Solving Right Triangles

To solve a right triangle means to find the lengths of all its sides and the measures of all its angles. This involves using the Pythagorean theorem, trigonometric ratios, and inverse trigonometric functions.

Example Problem

Given a right triangle where one leg is 5 units long and the hypotenuse is 13 units long, find the length of the other leg and the angles.

Solution:

Use the Pythagorean theorem:
5²+b²=13²
25+b²=169
b²=144
b=12
To find the angles, use trigonometric ratios:
$\sin \theta = \frac{5}{13} \Rightarrow \theta = \sin^{-1}\left(\frac{5}{13}\right)$
$\cos \theta = \frac{12}{13} \Rightarrow \theta = \cos^{-1}\left(\frac{12}{13}\right)$
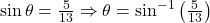
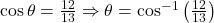
Thus, the angles are approximately 22.62° and 67.38°.

Unit Circle

The unit circle is a circle with a radius of one unit, centered at the origin of a coordinate plane. It is a valuable tool for understanding trigonometric functions. The coordinates of points on the unit circle correspond to the cosine and sine of the angles formed with the positive x-axis.

Key Angles

0° (0 radians): (1, 0)
90° 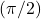$(\pi/2)$ radians: (0, 1)
180° 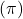$(\pi)$ radians: (-1, 0)
270° 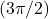$(3\pi/2)$ radians: (0, -1)

Trigonometric Identities

Several identities are useful for simplifying trigonometric expressions and solving equations:

Pythagorean Identity:
sin²θ+cos²θ=1
Sum and Difference Formulas:
sin(a±b) = sinacosb±cosasinb
cos(a±b) = cosacosb∓sinasinb

Applications of Trigonometry

Trigonometry has numerous real-world applications, including:

Architecture and Engineering: Designing structures, bridges, and machinery.
Physics: Analyzing wave motion, oscillations, and forces.
Astronomy: Measuring distances between celestial bodies.
Navigation: Determining positions using triangulation.

Examples

Example 1: Finding a Side Length

Given a right triangle with one leg of length 7 and an angle of 30°, find the length of the hypotenuse.

Solution:
$\cos(30°) = \frac{\text{adjacent}}{\text{hypotenuse}} = \frac{7}{h}$

$\frac{\sqrt{3}}{2} = \frac{7}{h}$

$h = \frac{7 \cdot 2}{\sqrt{3}} = \frac{14}{\sqrt{3}} \approx 8.08$

Example 2: Using the Pythagorean Theorem

A ladder 10 feet long leans against a wall. The base of the ladder is 6 feet from the wall. How high up the wall does the ladder reach?

Solution:
a²+b² = c²
6²+b² = 10²
36+b² = 100
b² = 64
b = 8
The ladder reaches 8 feet up the wall

Example 3: Finding an Angle

Given a right triangle with legs of lengths 5 and 12, find the angles other than the right angle.

Solution:
$\tan \theta = \frac{5}{12}$
$\theta = \tan^{-1}\left(\frac{5}{12}\right) \approx 22.62°$
The other angle is 90° – 22.62° = 67.38°.

Example 4: Special Right Triangle

In a 45°-45°-90° triangle, if one leg is 7 units long, find the length of the hypotenuse.

Solution:
$\text{Hypotenuse} = 7\sqrt{2} \approx 9.9$

Example 5: Unit Circle

Find the sine and cosine of 135° using the unit circle.

Solution:
135° corresponds to $\frac{3\pi}{4}$ radians.
$\sin 135° = \sin \left(\frac{3\pi}{4}\right) = \frac{\sqrt{2}}{2}$
$\cos 135° = \cos \left(\frac{3\pi}{4}\right) = -\frac{\sqrt{2}}{2}$

Practice Questions

Question 1

A right triangle has one leg of length 9 and a hypotenuse of length 15. What is the length of the other leg?

A) 6
B) 10
C) 12
D) 14

Answer: C

Explanation: Use the Pythagorean theorem.
9²+b²=15²
81+b²=225
b²=144
b=12

Question 2

In a 30°-60°-90° triangle, if the shorter leg is 5 units long, what is the length of the hypotenuse?

A) 5
B) 5√3
C) 10
D) 10√3

Answer: C

Explanation: In a 30°-60°-90° triangle, the hypotenuse is twice the length of the shorter leg.

Hypotenuse = 2×5 = 10

Question 3

What is the cosine of 60°?

A) 0.5
B) √3/2
C) 1
D) 0

Answer: A

Explanation: Using the definition of cosine in a 30°-60°-90° triangle or the unit circle,
cos60° = 0.5