Nonlinear Equations in One Variable and Systems of Equations in Two Variables

Nonlinear equations and systems of equations are fundamental topics in algebra and precalculus, frequently appearing on the Digital SAT Exam. Understanding how to solve nonlinear equations in one variable and systems of nonlinear equations in two variables is crucial for success. Nonlinear equations include quadratic, cubic, and higher-degree polynomial equations, as well as equations involving roots, exponential, and logarithmic functions. Systems of equations involve finding the common solutions to two or more equations, which can include both linear and nonlinear equations.

Learning Objectives

In this section, you will learn to solve nonlinear equations in one variable using various methods such as factoring, completing the square, and the quadratic formula. You will also learn to solve systems of equations in two variables by using substitution, elimination, and graphical methods. By mastering these skills, you will be able to tackle a wide range of problems on the Digital SAT Exam and apply these concepts to real-world scenarios.

Nonlinear Equations in One Variable

Solving Quadratic Equations

Quadratic equations are of the form ax²+bx+c=0, where a, b, and c are constants, and (a≠0) . Here are three methods to solve quadratic equations:

Factoring: Express the quadratic equation as a product of two binomials and set each binomial to zero.
- Example: Solve x²−5x+6=0 by factoring.
- (x−2)(x−3)=0
- Solutions: x=2 and x=3
Completing the Square: Rewrite the equation in the form (x−p)²=q and solve for x.
- Example: Solve x2−4x+1=0 by completing the square.
- x²−4x=−1
- x²−4x+4=3
- (x−2)²=3
- Solutions: \[( x = 2 \pm \sqrt{3})\]
Quadratic Formula: Use the formula 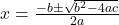\( x = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a}\) to find the roots.

Example: Solve 2x²−3x+1=0 using the quadratic formula.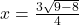

\(x=\frac{3±\sqrt{9-8}}{4}\)

Solutions: x=1 and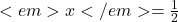 \(x=\frac{1}{2}\).

Solving Higher-Degree Polynomial Equations

Higher-degree polynomial equations, such as cubic and quartic equations, can be solved using methods like factoring, synthetic division, and the Rational Root Theorem. These equations can have multiple real and complex solutions.

Solving Equations Involving Roots

Equations involving roots, such as \( \sqrt{x + 2} = x – 1 \), can be solved by isolating the root and then squaring both sides to eliminate the root. It is important to check for extraneous solutions introduced by squaring.

Solving Exponential and Logarithmic Equations

Exponential equations can be solved by taking the logarithm of both sides, while logarithmic equations can be solved by exponentiating both sides.

Systems of Equations in Two Variables

Systems of equations involve solving for the values of variables that satisfy multiple equations simultaneously. They can be linear or nonlinear, and they can be solved using several methods.

Solving by Substitution

In the substitution method, solve one equation for one variable and substitute this expression into the other equation.

Example: Solve the system y=x²+1 and y=2x+3.

Substitute y=2x+3 into y=x²+1:
x²+1=2x+3
x²−2x−2=0
Solve the quadratic equation using the quadratic formula:
\[ x = 1 \pm \sqrt{3} \]
Substitute x back into y=2x+3 to find the corresponding y values.

Solving by Elimination

In the elimination method, add or subtract the equations to eliminate one variable, then solve for the remaining variable.

Example: Solve the system 2x+y=5 and x−y=1.
Add the equations:
2x+y+x−y=5+1
3x=6
x=2
Substitute x=2 into x−y=1:
2−y=1
y=1

Solving Graphically

Graphing the equations on the same set of axes can provide a visual solution. The points where the graphs intersect are the solutions to the system.

Examples of Nonlinear Equations in One Variable and Systems of Equations in Two Variables

Example 1

Quadratic Equation

Solve x²−4x−5=0.

Factoring:
- (x−5)(x+1)=0
- Solutions: x=5 and x=−1

Example 2

Cubic Equation

Solve x³−6x²+11x−6=0.

Factoring:
- (x−1)(x−2)(x−3)=0
- Solutions: x=1, x=2, and x=3

Example 3

Exponential Equation

Solve 2ˣ=8.

Take the logarithm of both sides:
- log(2ˣ)=log(8)
- xlog(2)=log(8)
- \[ x=\frac{log(8)}{log(2)}\]

Example 4

Logarithmic Equation

Solve log3(x)=2.

Rewrite in exponential form:
- 32=x
- x=9

Example 5

System of Equations

Solve y=x² and y=2x+3.

Substitute y=2x+3 into y=x²:
- x²=2x+3
- x²−2x−3=0
- (x−3)(x+1)=0
- Solutions: x=3, x=−1
- Corresponding y values: y=9, y=1

Practice Questions

Question 1

Solve the quadratic equation 2x²−8x+6=0 using the quadratic formula.

A) x=2,x=3

B) x=2,x=2

C) x=3,x=1

D) x=2,x=−2

Answer: C

Explanation:

Use the quadratic formula \[ x = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a} \].
a=2, b=−8, c=6
\[ x = \frac{8 \pm \sqrt{64 – 48}}{4} = \frac{8 \pm \sqrt{16}}{4} = \frac{8 \pm 4}{4} \]
x=3 and x=1

Question 2

Solve the system of equations:
y=x²+4
y=2x+1

A) (1,3) and (−1,3)

B) (1,3) and (2,5)

C) (1,2) and (−2,0)

D) (2,5) and (−3,−5)

Answer: B

Explanation: Substitute y=2x+1 into y=x2+4:
2x+1=x²+4.
Solve: x²−2x+3=0:
(x−1)(x−2)=0.
Solutions: x=1, x=2.
Substitute back: y=3, y=5.

Question 3

Which of the following represents the solution to the equation 2ˣ=16?

A) x=2

B) x=3

C) x=4

D) x=5