We strive to be our own persons. In the process of realizing our individual capacities, we would like to believe that the past does define our potential. But, to a degree, it does. Our family history will influence our lives. We may be able to sever parts of our ancestral ties, but our health and well-being will be among those threads that will always bind us to the ones that came before. When we know our family’s medical history, we can minimize the chance of a disease taking control of our lives.
[bb_toc content =”][/bb_toc]
Keeping track of our family tree and lineage is more than holding on to antiquated photos in albums and picture frames. Aside from being a manifestation of the human sentimentality and emotional attachment to the past, having knowledge of our ancestry, even just with the few closest generations, is a lifesaver. This is because family history records don’t just say who gave birth to whom. It also helps track hereditary diseases that, when left unattended, may debilitate a person. Family history questionnaires and pedigree are used in the medical community to assess the risks of individuals to different diseases and conditions. They help health professionals determine the patient’s risks to certain diseases.
Family History and Risk Management
The medical significance of tracking the family genogram came to light with the developments in medical genetics. The field deals with the role of genes and heredity in the health and well-being of a person. It is concerned with disorders that can be transmitted from the parent to offspring and succeeding generation. A person is more susceptible to diseases like diabetes, hypertension, heart problems, cancer, and mental disorders when his or her family is positive for these disorders. Because these diseases are at the genetic level, anyone can be vulnerable. But, having a family member with these illnesses increases the possibility of a person to develop these hereditary diseases in his or her lifetime.
In the case of diabetes, your genes carry your predisposition to develop the illness while its onset depends on your environment and lifestyle. Before a person is called a person with diabetes, he or she may already have a high blood sugar level. Although the amount is too small yet for the person to be diagnosed with the disease, the person should already exercise precautions to prevent diabetes. By knowing the likelihood to develop the disease from family history knowledge, early laboratory tests, and diabetes screening, the disease and its ill effects can be slowed down.
For several hereditary medical conditions, the most we could do is maintain a healthy lifestyle to reduce the likelihood of developing the disease. Preventive measures significantly reduce the probability, but there are still risks. Early detection of diseases is vital in controlling their manifestations and keeping the worse at bay. Family history evaluations are crucial in medical screening and prevention programs. By identifying a person’s risk factors as early as possible, we save him or her from the worst-case scenarios.
10+ Family History Questionnaire Examples
Even with the knowledge of family history’s potent role in reducing the risks of hereditary diseases and mitigating their manifestations, there is a lackluster implementation of tracking and recording of people’s genealogy. Inadequate screening and diagnosis lead to misinterpreted or undetected conditions and risks. How many people could have been saved when we treated family history recording with utmost urgency?
With the mentioned role of family history in primary care, the medical field should give importance to the detailed collection, filing, and interpretation of these records. Health care providers use family history records and health assessment forms to evaluate a person’s inherited health risks. Upon detection, doctors can advise the patient on what he or she can do to minimize the possibility of the disease. Physicians can also refer to these forms along with the patients’ test results to perform the correct diagnosis. Browse through our extensive list of family history questionnaires that you can adapt for your clinic and hospital operations.
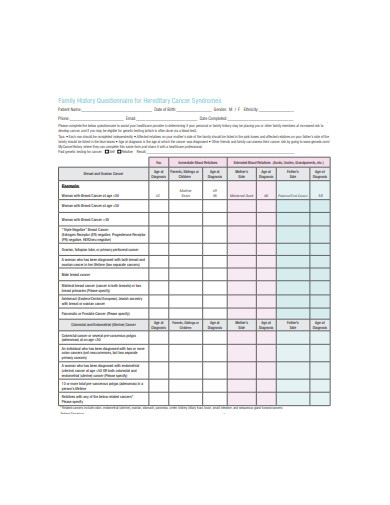
1. Family History Questionnaire for Hereditary Cancer
2. Family History Screening Questionnaire Checklist
3. Cancer Genetics Services Family History Questionnaire
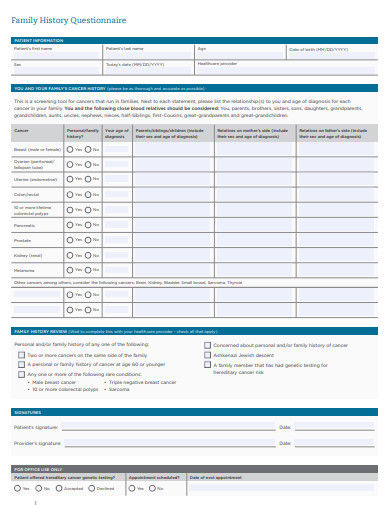
4. Personal and Family History Questionnaire
5. Family History Questionnaire for Cancer
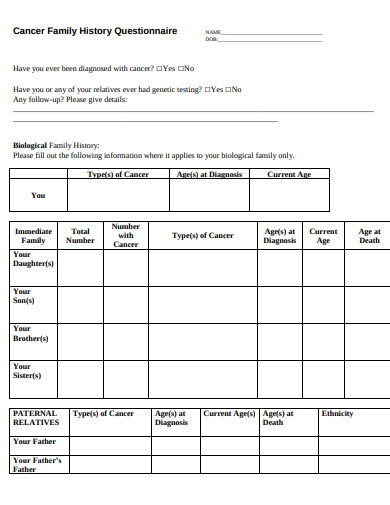
6. Cancer Family History Questionnaire
7. Family History Questionnaire Checklist
8. Family History Questionnaire for Student
9. Family Health History Questionnaire Form Example
10. Prenatal Family Health History Questionnaire
11. Family History Interview Questionnaire
Maximizing Questionnaire Potential
The questionnaires are clinical assessment tools used to check for a person’s chances to develop hereditary diseases. Physicians then advice patients on what they can do about the situation. To maximize the questionnaires’ benefits, its construction should have the its goal in mind. How do you utilize the questionnaire to its full medical screening potential?
1. It is People-Friendly
First and foremost, it is the patient who will fill out the form. They should not find it difficult to use the questionnaire. Even if the patient is likely to fill in the questionnaire in the hospital or clinic with a medical personnel close by, the content should still be understandable to an average person. The person writing on the form may not have much medical knowledge to understand technical jargons. The questionnaire you will use in the clinic should consider the literacy and competency of the local population. If need be, assume the native tongue in the instructions.
2. It is Open to Changes
There is a saying that whenever something is published, it starts to become obsolete. In a similar manner, what is written in the questionnaires may not remain the true state of a person’s health. Human health and life are dynamic. They are always changing. New information may come to light from unearthing old documents in the attic, or new laboratory results indicating a misinterpretation of the symptoms. Therefore, your questionnaires should accommodate these updates and changes. New patients may come back for another medical appointment bearing the new information. The forms should have room for the new data.
3. People Understand its Value
It is hard to campaign for better documentation of patients’ family history when the patients themselves aren’t aware of the medical benefits of knowing their family tree. While there are online blogs advocating for caring about one’s family history, not everyone gets to read this. There should be a wide information dissemination about the significance of this knowledge and the advantage of knowing your risks. When people understand the importance of knowing why these data are relevant to disease prevention, they will make an effort to collect and relay the information to their doctors. Improving health care involves the coordination of the medical community and the public.
4. It has a Centralized System
Instead of building a tall pile of papers which makes file retrieval difficult and unpleasant, hospitals and clinics should consider adapting electronic means of storing and retrieving documents. By entering the patients’ information from the physical questionnaire into a database, it will be easier to track and review the patients’ profiles. With a few clicks of buttons, the entire medical history of a person is ready for review. It is also easier to keep track of changes over time.
Family history will have a say in our lives in terms of our health. We can’t choose our lineage, but we can make do with what we have. When we know our risks, we can exercise preventive and cautionary measures. When we take action at the earliest possible time, we have a bigger window of opportunity to arm ourselves against possible diseases. We have more time to shift to a healthier lifestyle, eat better, and control our vices. We can approach doctors and see what preventive treatment should we consider. Family history records, then, are both a medical screening and cautionary tool. It is not a perfect instrument, but it can extend our lives.