Understanding lines, angles, and triangles is fundamental in geometry and is crucial for performing well on the Digital SAT Exam. This topic forms the basis for more complex geometric concepts and appears frequently in various problems. Lines and angles are the building blocks of shapes, while triangles, as the simplest polygons, offer a wealth of properties and relationships to explore. Mastering these concepts will not only help in solving geometry problems but also enhance logical thinking and problem-solving skills.
Learning Objectives
In this section, you will learn to identify and classify different types of lines, angles, and triangles, understand their properties, and solve related problems. By the end of this section, you will be able to apply these concepts to various geometric problems on the Digital SAT Exam.
Lines
Lines are the simplest geometric figures, extending infinitely in both directions without any curvature. They are defined by two points through which they pass. Lines can be used to describe various geometric shapes and forms and are the basis for defining angles and other shapes. In coordinate geometry, lines can be represented using linear equations.
Types of Lines

- Line: Extends infinitely in both directions.
- Line Segment: Has two endpoints and a definite length.
- Ray: Has one endpoint and extends infinitely in one direction.
Relationships Between Lines
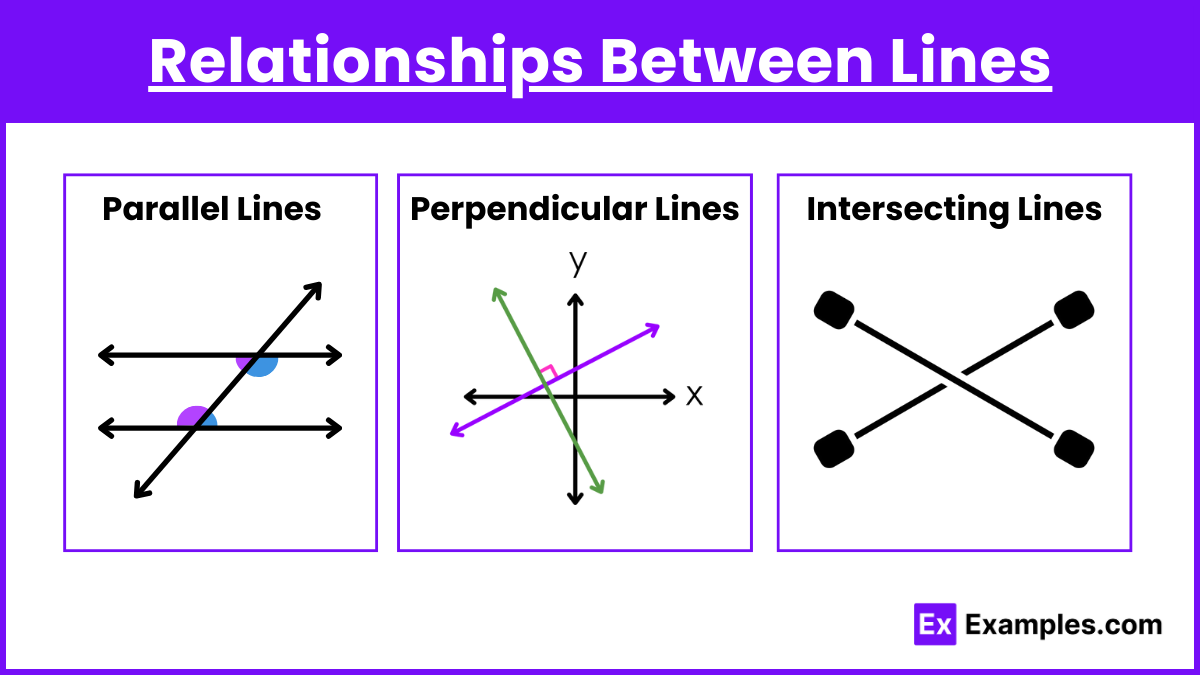
- Parallel Lines: Two lines that never intersect and are always the same distance apart.
- Perpendicular Lines: Two lines that intersect at a right angle (90 degrees).
- Intersecting Lines: Two lines that cross each other at any angle other than 90 degrees.
Angles
Angles are formed by two rays (or line segments) that share a common endpoint, known as the vertex. Angles are measured in degrees, which describe the amount of rotation from one ray to the other around their common endpoint. Angles are essential in defining shapes and understanding their properties.
Types of Angles
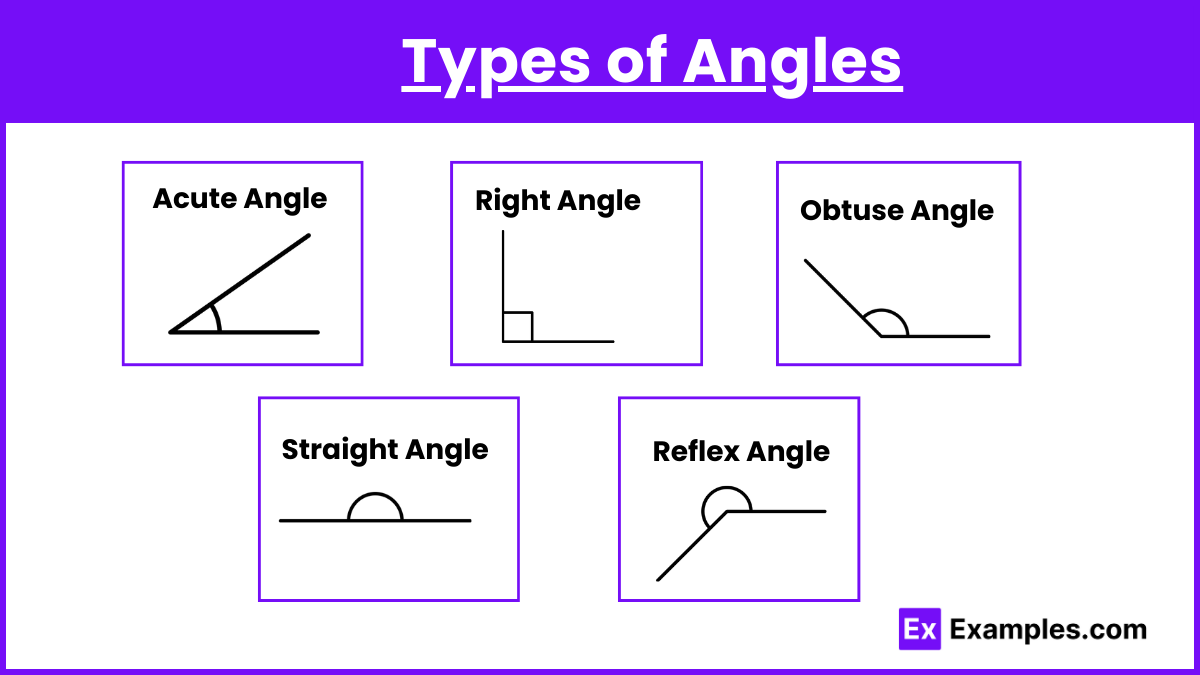
- Acute Angle: Less than 90 degrees.
- Right Angle: Exactly 90 degrees.
- Obtuse Angle: More than 90 degrees but less than 180 degrees.
- Straight Angle: Exactly 180 degrees.
- Reflex Angle: More than 180 degrees but less than 360 degrees.
Angle Relationships

- Complementary Angles: Two angles that add up to 90 degrees.
- Supplementary Angles: Two angles that add up to 180 degrees.
- Adjacent Angles: Two angles that share a common side and vertex.
- Vertical Angles: Opposite angles formed by two intersecting lines; they are equal.
- Alternate Interior Angles: Angles on opposite sides of a transversal but inside the parallel lines; they are equal.
- Corresponding Angles: Angles in matching positions when a transversal crosses two lines; they are equal if the lines are parallel.
Triangles
Triangles are three-sided polygons that are classified based on their side lengths and angles. They are the simplest polygons and serve as building blocks for more complex shapes. Understanding triangles involves studying their types, properties, and theorems related to their angles and sides.
Types of Triangles by Sides
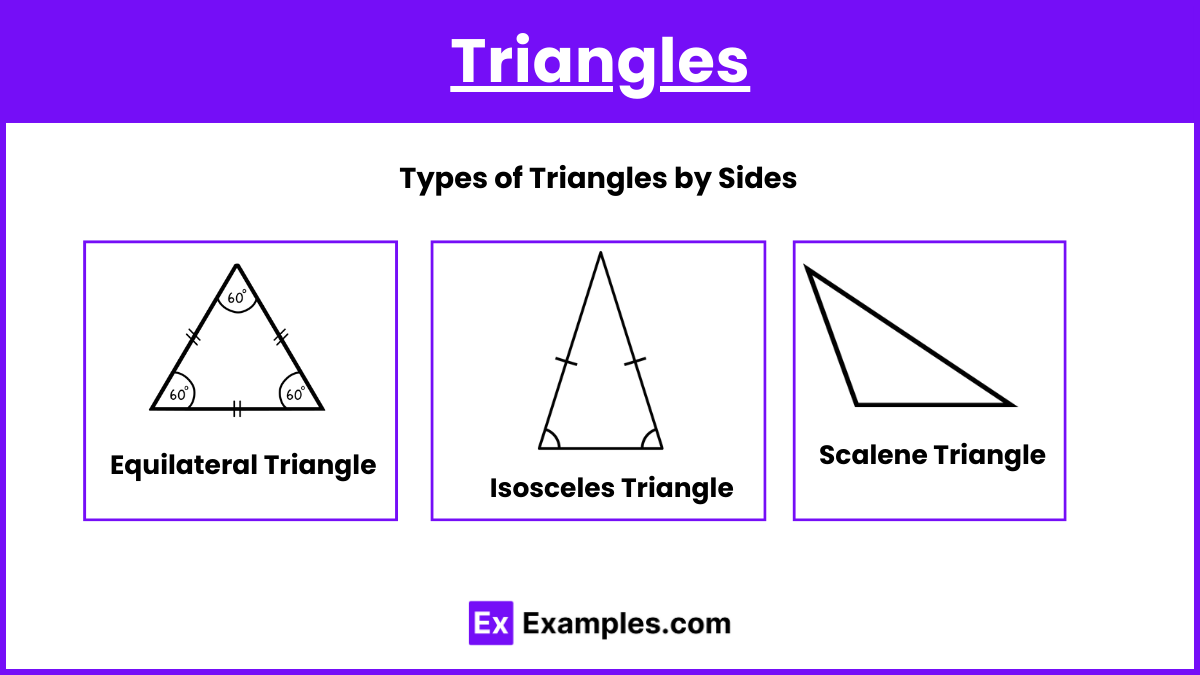
- Equilateral Triangle: All three sides are equal, and all angles are 60 degrees.
- Isosceles Triangle: Two sides are equal, and the angles opposite these sides are equal.
- Scalene Triangle: All sides and angles are different.
Types of Triangles by Angles
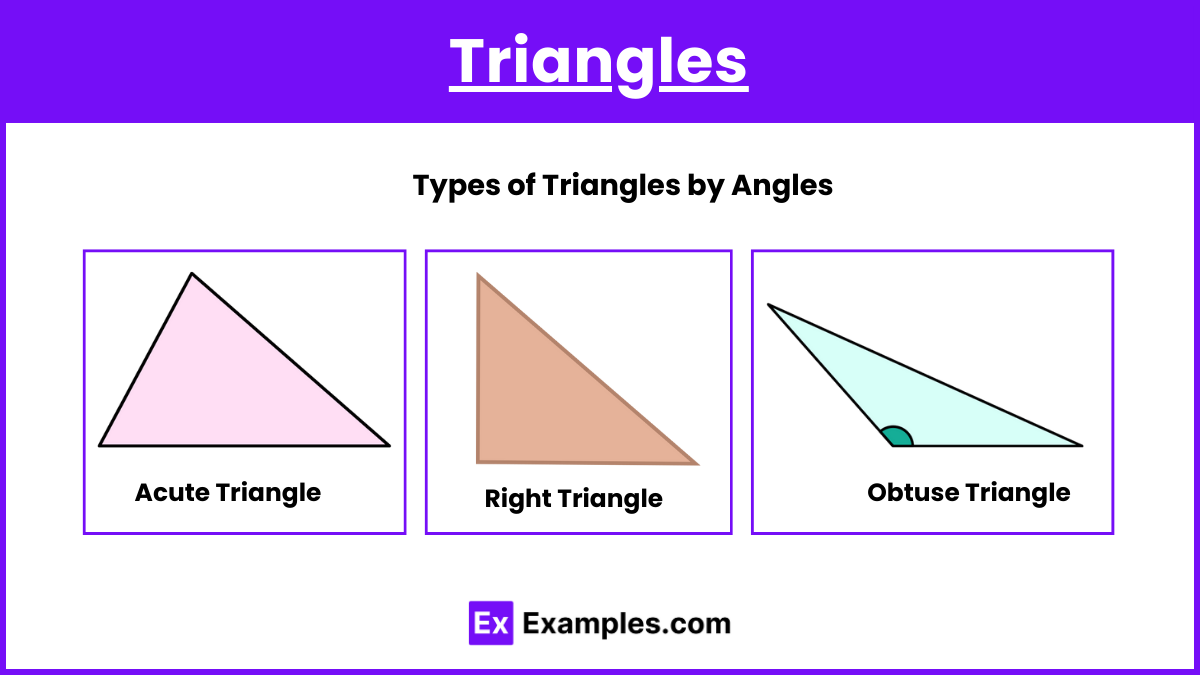
- Acute Triangle: All three angles are less than 90 degrees.
- Right Triangle: One angle is exactly 90 degrees.
- Obtuse Triangle: One angle is more than 90 degrees.
Properties of Triangles
- Sum of Interior Angles: The sum of the interior angles of a triangle is always 180 degrees.
- Exterior Angle Theorem: An exterior angle of a triangle is equal to the sum of the two non-adjacent interior angles.
- Triangle Inequality Theorem: The sum of the lengths of any two sides of a triangle is greater than the length of the third side.
Examples of Lines, Angles, and Triangles
Example 1: Identifying Angles
Given two parallel lines cut by a transversal, if one of the alternate interior angles is 65 degrees, find the other alternate interior angle.
Solution: Since the lines are parallel, the alternate interior angles are equal. Therefore, the other alternate interior angle is also 65 degrees.
Example 2: Finding a Missing Angle in a Triangle
In a triangle, if two angles are 45 degrees and 55 degrees, find the third angle.
Solution: Using the sum of interior angles in a triangle:
45+55+third angle = 180
100+third angl e= 180
third angle = 180−100 = 80
So, the third angle is 80 degrees.
Example 3: Classifying Triangles by Sides
A triangle has sides of lengths 5 cm, 5 cm, and 8 cm. Classify the triangle by its sides.
Solution: Since two sides are equal, the triangle is an isosceles triangle.
Example 4: Using the Exterior Angle Theorem
In a triangle, the exterior angle is 120 degrees, and one of the non-adjacent interior angles is 45 degrees. Find the other non-adjacent interior angle.
Solution: Using the exterior angle theorem:
Exterior angle = Sum of non-adjacent interior angles
120 = 45+other interior angle
other interior angle = 120−45=75
So, the other interior angle is 75 degrees.
Example 5: Applying the Triangle Inequality Theorem
Can a triangle have sides of lengths 7 cm, 10 cm, and 18 cm?
Solution: Using the triangle inequality theorem:
7+10>18→17>18 (False)
7+18>10→25>10 (True)
10+18>7→28>7 (True)
Since one of the inequalities is false, a triangle with these side lengths is not possible.
Practice Questions
Question 1
Which of the following pairs of angles are complementary?
A) 45 degrees and 45 degrees
B) 60 degrees and 30 degrees
C) 90 degrees and 90 degrees
D) 120 degrees and 60 degrees
Answer: B
Explanation: Complementary angles add up to 90 degrees. Here, 60 degrees + 30 degrees = 90 degrees.
Question 2
If a triangle has one angle measuring 90 degrees and another angle measuring 30 degrees, what is the measure of the third angle?
A) 30 degrees
B) 60 degrees
C) 90 degrees
D) 120 degrees
Answer: B
Explanation: The sum of the interior angles of a triangle is 180 degrees. Since one angle is 90 degrees and another is 30 degrees, the third angle is 180−90−30=60 degrees.
Question 3
In the diagram, two parallel lines are cut by a transversal. One of the corresponding angles is 75 degrees. What is the measure of the corresponding angle on the other parallel line?
A) 75 degrees
B) 105 degrees
C) 115 degrees
D) 125 degrees
Answer: A
Explanation: Corresponding angles are equal when two parallel lines are cut by a transversal. Therefore, the corresponding angle on the other parallel line is also 75 degrees.


