Circles

Last Updated: September 25, 2024

Notes

Circles are fundamental geometric shapes that play a significant role in various fields of mathematics, particularly in geometry and trigonometry. Understanding circles is crucial for performing well on the Digital SAT Exam, as they frequently appear in both the math section and in problem-solving scenarios. A circle is defined as the set of all points in a plane that are equidistant from a fixed point called the center. This distance from the center to any point on the circle is known as the radius. Circles exhibit unique properties and have several important components, including the diameter, circumference, and area.

Learning Objectives

In this section, you will learn to identify and analyze different properties and components of circles, understand their equations, and solve problems involving circles. You will also learn to apply these concepts to real-world situations and various types of mathematical problems. By the end of this section, you will be able to confidently work with circles on the Digital SAT Exam.

Basic Properties of Circles

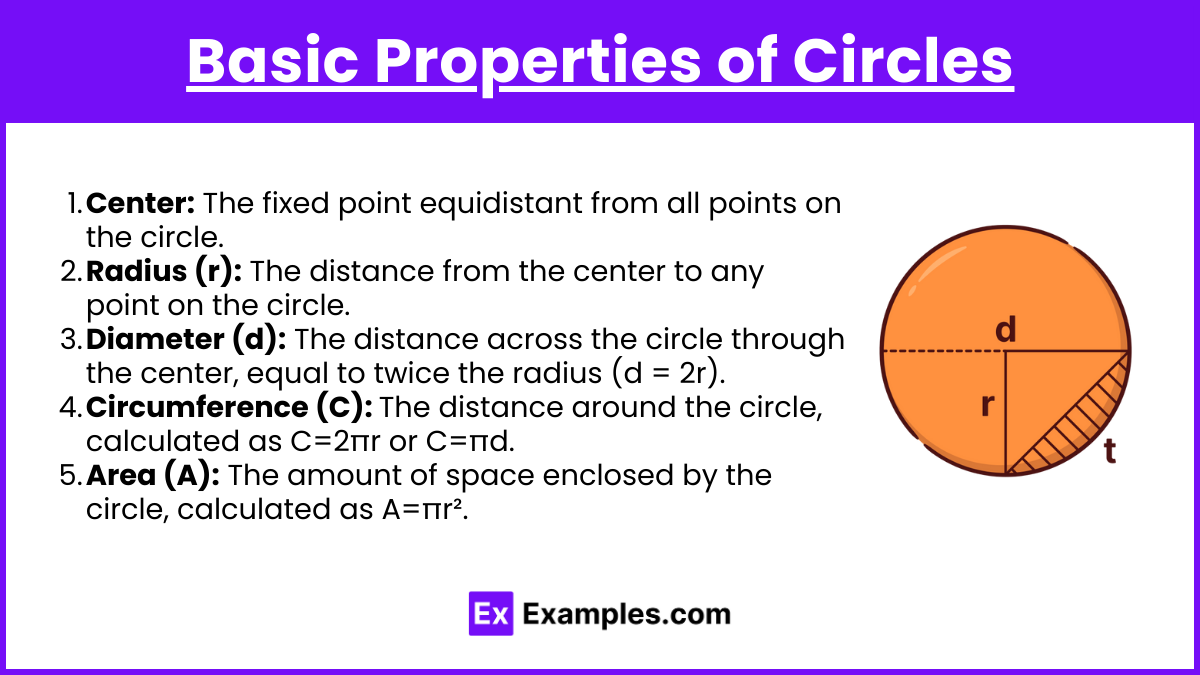
Center: The fixed point equidistant from all points on the circle.
Radius (r): The distance from the center to any point on the circle.
Diameter (d): The distance across the circle through the center, equal to twice the radius (d = 2r).
Circumference (C): The distance around the circle, calculated as C=2πr or C=πd.
Area (A): The amount of space enclosed by the circle, calculated as A=πr².

Equations of a Circle

The standard equation of a circle with center at (h, k) and radius r is:
(x−h)²+(y−k)² = r²

For a circle centered at the origin (0, 0), the equation simplifies to:
x²+y²=r²

Important Components and Terms

Chord: A line segment with both endpoints on the circle.
Secant: A line that intersects the circle at two points.
Tangent: A line that touches the circle at exactly one point, known as the point of tangency.
Arc: A part of the circumference of a circle.
Central Angle: An angle whose vertex is the center of the circle and whose sides are radii.
Inscribed Angle: An angle formed by two chords with the vertex on the circle.

Properties of Arcs and Angles

Arc Length: The distance along the curved line making up the arc. For a circle with radius r and a central angle θ (in radians), the arc length s is given by s=rθ.
Sector Area: The area of a portion of the circle enclosed by two radii and the corresponding arc. For a central angle θ (in radians), the sector area A is given by $A = \frac{1}{2}r^2\theta$ .

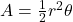Circles in Coordinate Geometry

To determine if a point (x, y) lies on a circle with center (h, k) and radius r, check if (x−h)²+(y−k)²=r².
The distance formula, 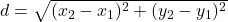$d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$ , is useful for finding the distance between points, which can help determine relationships between circles and other geometric figures.

Examples of Circles

Example 1: Equation of a Circle

Find the equation of a circle with center at (3, -2) and radius 5.

(x−3)²+(y+2)² = 25

Example 2: Radius and Diameter

A circle has a diameter of 10 units. What is its radius?

Since the diameter is twice the radius, the radius is $\frac{10}{2} = 5$ units.

Example 3: Circumference

Calculate the circumference of a circle with a radius of 7 units.

C = 2πr = 2π×7 = 14π

Example 4: Area

Find the area of a circle with a radius of 4 units.

A = πr² = π×4² = 16π

Example 5: Point on a Circle

Determine if the point (5, -1) lies on the circle with center at (2, 3) and radius 5.

Check if (x−2)²+(y−3)²=25:

(5−2)²+(−1−3)²=3²+(−4)²=9+16=25

Since 25 equals the radius squared, the point lies on the circle.

Practice Questions

Question 1

What is the equation of a circle with center at (1, -3) and radius 4?

A) (x+1)²+(y−3)²=16

B) (x−1)²+(y+3)²=16

C) (x−1)²+(y−3)²=16

D) (x+1)²+(y+3)²=16

Answer: B

Explanation: The standard form of the equation of a circle is (x−h)²+(y−k)²=r². Here, h=1, k=−3, and r=4. Substituting these values, we get (x−1)²+(y+3)²=16.

Question 2

What is the length of the radius of a circle with an area of 49π square units?

A) 5

B) 6

C) 7

D) 8

Answer: C

Explanation: The area of a circle is given by A=πr². Given that the area is 49π, we have πr²=49π. Dividing both sides by π, we get r²=49, so r=7.

Question 3

If the circumference of a circle is 18π units, what is the diameter?

A) 9

B) 12

C) 18

D) 36

Answer: C

Explanation: The circumference of a circle is given by C=πd. Given that the circumference is 18π, we have πd=18π. Dividing both sides by π, we get d=18.