Square & Square root of 1
Square of 1
To calculate the square of 1, you simply multiply 1 by itself:
Therefore, the square of 1 is 1. This straightforward calculation is a building block for more complex mathematical operations and concepts, including algebraic equations, geometric formulas, and statistical models.
Square Root of 1
The square root of 1 is simply 1. This is because the square root operation asks the question, “What number, when multiplied by itself, gives the original number?” For the case of 1, multiplying 1 by itself (1 × 1) yields 1. Mathematically, this is expressed as 1=11=1. The concept is straightforward and serves as a fundamental example of how square roots work, illustrating that the square root of a positive number can be positive (and in this unique case, the same as the original number).
Exponential Form: 1^1/2 or 1^0.5
Radical Form: √1
Is the Square Root of 1 Rational or Irrational?
- A rational number is any number that can be expressed as a fraction a/b where a and b are integers, and b is not equal to zero. It includes integers, fractions, and finite or repeating decimals.
- An irrational number is a number that cannot be expressed as a simple fraction. Irrational numbers have non-repeating, non-terminating decimal expansions.
A rational number is defined as a number that can be expressed as the fraction a/b where a and b are integers, and b is not zero. The square root of 1 is exactly 1 (√1=1), which can be expressed as a fraction like 1/1, fitting the definition of a rational number perfectly.
Methods to Find Value of Root 1
To find the value of the square root of 1 (√1) , you can follow this straightforward approach:
- Understand what square root means: The square root of a number is a value that, when multiplied by itself, gives the original number.
- Apply this to 1: Ask yourself, “What number times itself equals 1?” The answer is simple: 1, because 1×1=1.
Square Root of 1 by Long Division Method
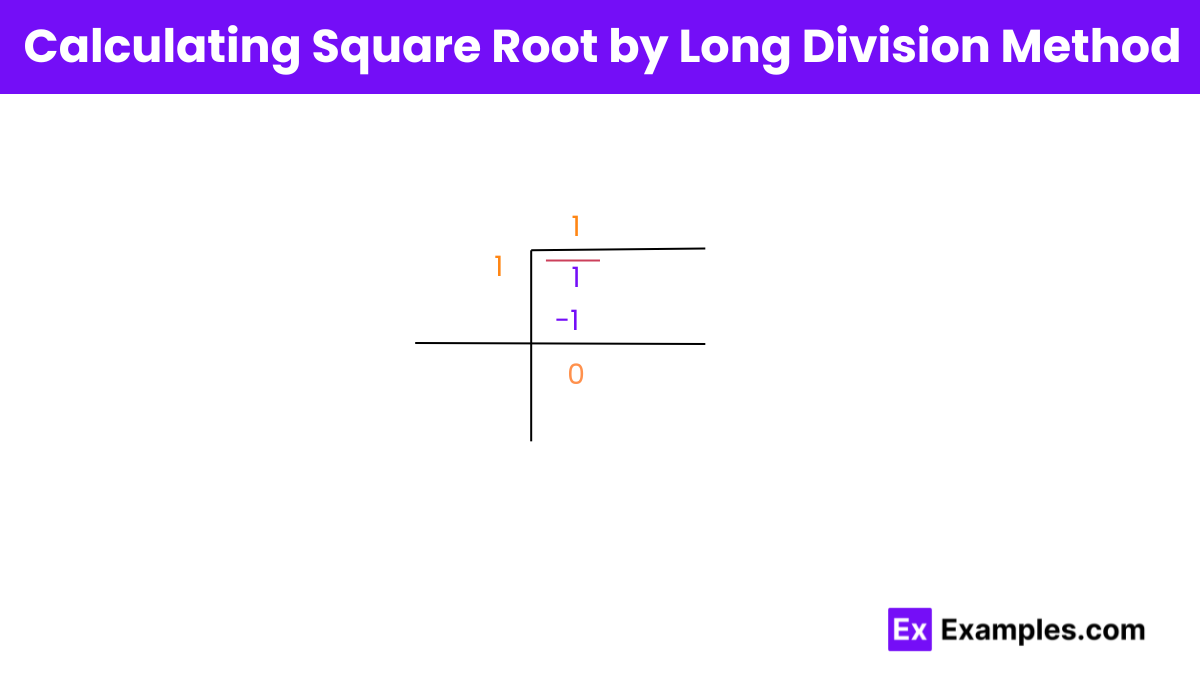
Square Root of 1 (√1):
Recognize the operation: Understand that finding the square root of a number involves determining the number that, when multiplied by itself, equals the original number.
Compute: Calculate the square root of 1. Since 1×1 = 1, the square root of 1 is 1.
Interpretation: This means that the length of each side of a square with an area of 1 square unit is 1 unit.
Check: Verify the result by squaring the calculated square root. In this case, 1×1 = 1, confirming that the square root of 1 is indeed 1.
1 is Perfect Square root or Not
The square root of 1 is 1, because 1×1=1. A perfect square is a number that can be expressed as the product of an integer with itself.
FAQ’S
What is the square root of a negative 1?
The square root of negative 1 is defined as “i”, where “i” is the imaginary unit. It satisfies the equation i² = -1, a foundational concept in complex numbers.
Can √ 1 be a value?
Yes, √1 can be a value. The square root of 1 is 1, because 1 squared (1×1) equals 1. It satisfies the definition of a square root.
Why is √ 1 imaginary?
√1 is not imaginary; it is real and equals 1. The confusion might arise with √-1, which is imaginary, denoted as i, defining the basis for complex numbers.
Share :
