What is the square of 156?
24,336
22,656
25,236
23,136


Within the realm of algebraic mathematics, squares and square roots are fundamental concepts. Squaring a number, like 156, involves multiplying it by itself, yielding 24336. This foundational operation is crucial for exploring rational and irrational numbers. Understanding these basics enriches comprehension of mathematical relationships and patterns. Squares reveal inherent number properties, while square roots unravel intricate numerical mysteries. These concepts serve as guiding lights, illuminating mathematical landscapes and enabling explorations into fractional territories. Proficiency in squares and square roots equips mathematicians to navigate diverse mathematical terrains, unveiling the elegance and complexity inherent within algebraic frameworks.
The square of 156 equals 24,336, obtained by multiplying 156 by itself, a foundational operation in algebraic mathematics, revealing inherent number properties.
Or
√156 ≈ 12.489 upto 3 decimals
The square root of 156 is approximately 12.489. This fundamental mathematical operation reveals the value that, when multiplied by itself, equals 156.
Exponential Form: 156^½ or 156^0.5
Radical Form: √156
Rational numbers are expressible as the quotient of two integers.
Irrational numbers, however, cannot be represented as fractions of integers. Examples of irrational numbers include the square roots of non-perfect squares.
Prime Factorization Method: Break down 156 into its prime factors. However, since 156 is not a perfect square, its prime factorization results in a mixture of prime factors.
Long Division Method: Utilize the long division algorithm to approximate the square root of 156 iteratively.
Using a Calculator: Most calculators are equipped with a square root function, enabling direct calculation of the square root of 156.
Estimation: As 156 falls between the perfect squares of 144 (12 × 12) and 169 (13 × 13), an estimate can be made that its square root is likely between 12 and 13, closer to 12.
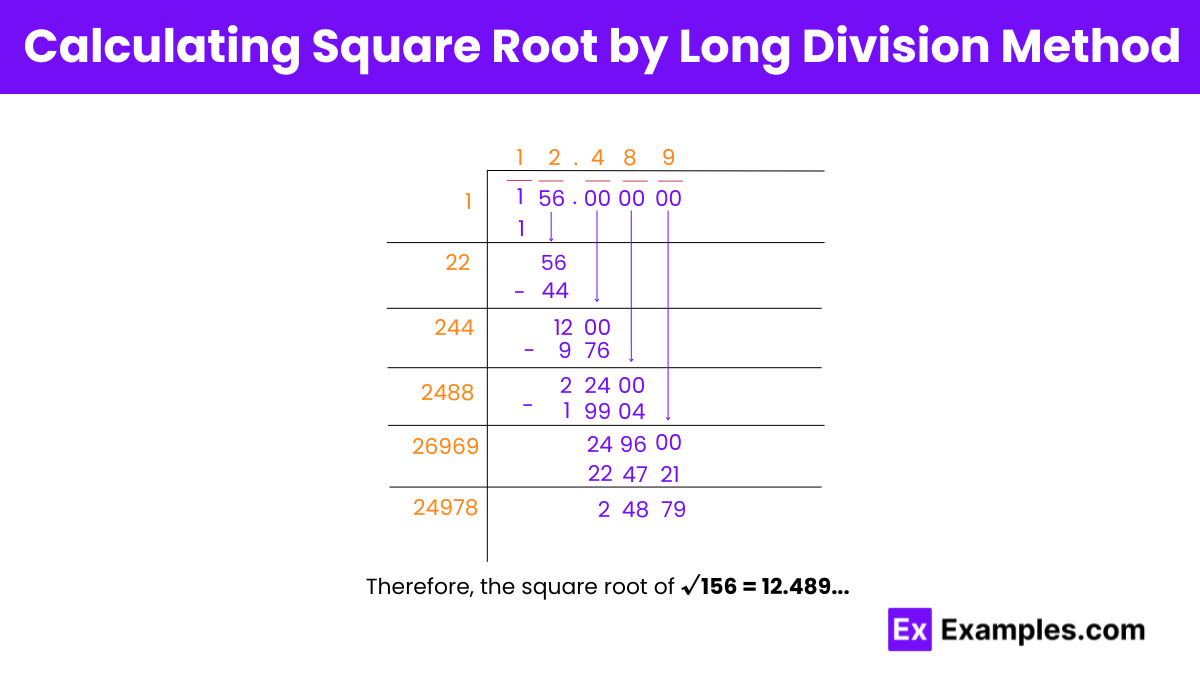
Step 1: Form pairs: 01 and 56.
Step 2: Find Y (1) such that 1² ≤ 01. Divide 01 by 1, quotient = 1.
Step 3: Bring down 56, making the new dividend 156. Add quotient’s last digit to divisor (1 + 1 = 2).
Step 4: Find Z (2) such that 22Z × Z ≤ 56. Form new divisor 22Z (22).
Step 5: Divide 156 by 22, quotient = 2, remainder = 12.
Step 6: Bring down 00, new dividend = 1200. Add last digit of quotient to divisor (2 + 22 = 24).
Step 7: Find Z (4) such that 244Z × Z ≤ 1200. New divisor = 244Z (244).
Step 8: Divide 1200 by 244, quotient = 4, remainder = 224.
Step 9: Repeat for more decimal places to find the square root of 156.
A perfect square cannot be expressed as the square of an integer. Therefore, the square root of 156 is an irrational number.
No, 156 is not a perfect cube. Its cube root is approximately 5.33, which is not an integer, indicating that 156 cannot be expressed as the cube of an integer.
156 is divisible by 1, 2, 3, 4, 6, 12, 13, 26, 39, 52, 78, and 156. These are its factors, which include both prime and composite numbers.
The square root of 156 cannot be simplified by prime factorization as 156 = 2² × 3 × 13, and it does not have a pair for 3 and 13. Thus, √156 remains √(2² × 3 × 13).
The number 156 in index form is represented by its prime factorization: 2² × 3 × 13. This notation breaks down 156 into its prime factors with their respective exponents.
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What is the square of 156?
24,336
22,656
25,236
23,136
What is the approximate value of the square root of 156?
12.4
12.6
12.8
13
Which number is closest to the square root of 156?
12
13
14
15
If x² = 156, what is the value of x?
12
13
12.49
15
What is the square root of 156 to two decimal places?
12.45
12.47
12.49
12.51
What is 156 squared plus 1?
22,657
22,658
22,659
22,660
What is the difference between the square of 156 and 156?
22,500
22,600
22,656
22,800
If the square of a number is 156, what is the number?
12.5
12.49
13
13.2
What is the product of the square root of 156 and 10?
124.9
126.0
129.0
130.0
What is the nearest whole number to the square root of 156?
12
13
14
15
Before you leave, take our quick quiz to enhance your learning!

