Square & Square Root of 1089

Within the realm of algebraic mathematics, squares and square roots are pivotal concepts. Squaring a number, like 1089, involves multiplying it by itself, yielding 1,188,321. This operation is foundational, crucial in exploring rational and irrational numbers. Understanding these basics enriches comprehension of mathematical relationships and patterns. Squares reveal inherent properties of numbers, while square roots unravel complex numerical mysteries. These concepts illuminate mathematical landscapes, guiding explorations into fractional territories. Mastery of squares and square roots empowers mathematicians to navigate diverse mathematical terrains, uncovering the elegance and complexity woven within algebraic frameworks.

Square of 1089

1089² (1089 × 1089) = 1,188,321

The square number 1089 equals 1,188,321, derived by multiplying 1089 by itself, a fundamental operation in algebraic mathematics, revealing inherent properties of numbers.

Square Root of 1089

√1089 = 33

The square root of 1089 is 33. This fundamental operation in mathematics uncovers the value that, when multiplied by itself, equals 1089.

Square Root of 1089 : 33

Exponential Form : 1089^½ or 1089^0.5

Radical Form : √1089

Is the Square Root of 1089 Rational or Irrational?

Yes, the square root of 1089 is a rational number.

Rational Numbers : Rational numbers are those that can be expressed as the quotient of two integers, where the denominator is not zero. In other words, they can be written as fractions of the form a/b where (a) and (b) are integers and (b ≠ 0). Rational numbers include integers and fractions. Examples of rational numbers include 1/2, -3, and 5/7.

Irrational Numbers : Irrational numbers cannot be expressed as fractions of integers. Their decimal representations are non-repeating and non-terminating. These numbers cannot be represented as finite or repeating decimals. Examples of irrational numbers include the square roots of non-perfect squares like √2, √3, and √5, as well as transcendental numbers like π.

Methods to Find Value of Root 1089

Prime Factorization Method: Break down 1089 into its prime factors, which are 3 × 3 × 11 × 11. Since the square root of 1089 is 33, it’s the product of the prime factors in pairs: (3 × 11) = 33.

Long Division Method : Use the long division algorithm to find the square root of 1089 by approximation. Start with a guess (e.g., 30) and refine iteratively.

Using a Calculator : Most calculators have a square root function. Simply input 1089 and find the square root directly.

Estimation : Since 1089 is close to the perfect square of 1024 (32 × 32) and 1156 (34 × 34), you can estimate that its square root is likely between 32 and 34, closer to 33.

Square Root of 1089 by Long Division Method

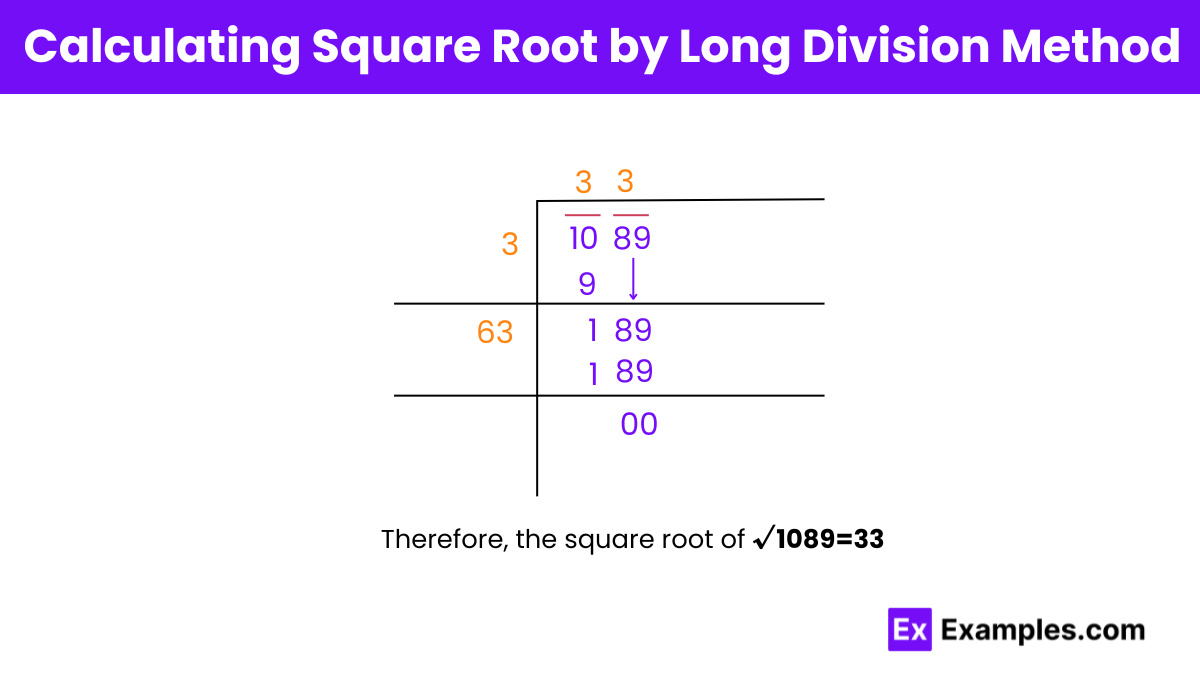
Step 1: Forming pairs: 10 and 89
Step 2: Find a number Y (3) such that its square is less than or equal to 10. Now divide 10 by 3 with the quotient as 3.
Step 3: Bring down the next pair 89, to the right of the remainder 1. The new dividend is now 189.
Step 4: Add the last digit of the quotient (3) to the divisor (3) i.e. 3 + 3 = 6. To the right of 6, find a digit Z (which is 3) such that 63 × Z is less than or equal to 189. After finding Z, together 6 and Z (3) form a new divisor 63 for the new dividend 189.
Step 5: Divide 189 by 63 with the quotient as 3, giving the remainder = 189 – 63 × 3 = 189 – 189 = 0.
We stop the process since the remainder is now 0 and there are no more digits that can be brought down.

Is 1089 a Perfect Square root or Not

Yes, the number 1089 is a perfect square

Yes, 1089 is a perfect square because it can be expressed as the square of an integer, specifically (33 × 33), which equals 1089. Therefore, the square root of 1089 is a whole number (33), making it a perfect square.