Square & Square Root of 101
Square & Square Root of 101
Within the realm of algebraic mathematics, squares and square roots are fundamental concepts. Squaring 101 yields 10,201, essential for understanding rational and irrational numbers. Mastery of these concepts illuminates mathematical relationships, aiding navigation through algebraic frameworks.
Square of 101
Square number of 101 is multiplying 101 by itself equals 10,201, a foundational operation in algebraic mathematics.
Square Root of 101
Or
√101 ≈ 10.049 upto 3 decimals
The square root of 101 is approximately 10.05, revealing the value that, when multiplied by itself, equals 101.
Exponential Form: 101^½ or 101^0.5
Radical Form: √101
Is the Square Root of 101 Rational or Irrational?
Rational numbers can be expressed as fractions of integers, while irrational numbers cannot.
Methods to Find the Square Root of 101
Prime Factorization Method: Break down 101 into prime factors.
Long Division Method: Utilize long division to approximate the square root of 101.
Using a Calculator: Most calculators provide a square root function.
Estimation: As 101 falls between the perfect squares of 100 (10 × 10) and 121 (11 × 11), its square root is approximately 10, closer to 10.
Square Root of 175 by Long Division Method
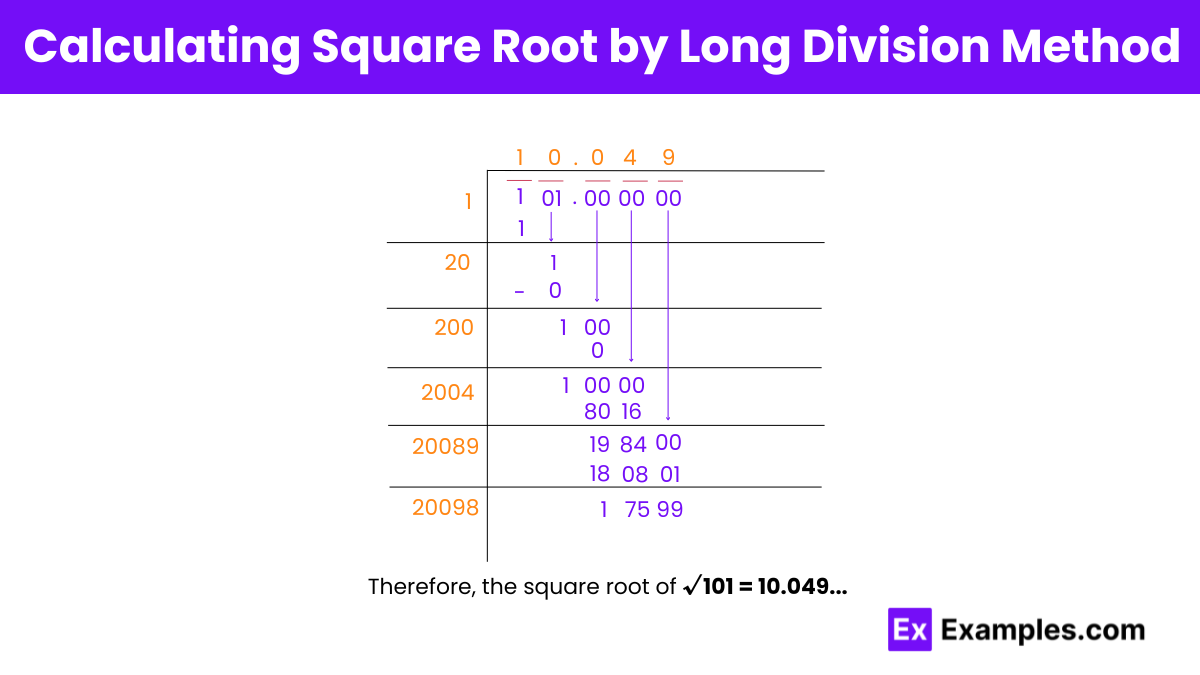
Step 1: Pair the digits of 101 starting with a digit at one’s place, indicated by a horizontal bar.
Step 2: Find a number whose square is less than or equal to 1. Since 1 × 1 = 1, we use 1 as the starting digit of the quotient.
Step 3: Bring down 01 and multiply the quotient by 2, yielding 2. This becomes the starting digit of the new divisor.
Step 4: Place 0 at the one’s place of the new divisor. When 20 is multiplied by 0, we get 0. The quotient now becomes 1, and we bring down 00.
Step 5: Multiply the quotient (10) by 2, resulting in 20, which becomes the starting digit of the new divisor.
Step 6: Place 0 at the one’s place of the new divisor. When 200 is multiplied by 0, we get 0. The quotient now becomes 100, and we bring down 00.
Step 7: Multiply the quotient (100) by 2, resulting in 200, which becomes the starting digit of the new divisor.
Step 8: Place 4 at the one’s place of the new divisor. When 2004 is multiplied by 4, we get 8016. The quotient now becomes 1984, and we bring down 00.
Step 9: Multiply the quotient (1004) by 2, resulting in 2008, which becomes the starting digit of the new divisor.
Step 10: Place 9 at the one’s place of the divisor. When 20089 is multiplied by 9, we get 180801. The quotient now becomes 17599.
Is 101 a Perfect Square?
Perfect square cannot be expressed as the square of an integer.
Can the square root of 101 be simplified?
No, the square root of 101 cannot be simplified because it is an irrational number, meaning it cannot be expressed as a fraction of integers.
What is the cube root of 101?
The cube root of 101 is approximately 4.682. This value represents the number that, when multiplied by itself twice, equals 101.
Can the square root of 101 be expressed as a fraction?
No, the square root of 101 cannot be expressed as a fraction because it is an irrational number, meaning its decimal representation neither terminates nor repeats.
Share :
