Square & Square Root of 175
Square & Square Root of 175
Within the domain of algebraic mathematics, squares and square roots hold significant importance. Squaring a number, such as 175, entails multiplying it by itself, yielding 30625. This foundational operation is vital for exploring rational and irrational numbers. A grasp of these fundamentals enriches understanding of mathematical relationships and patterns. Squares illuminate inherent number properties, while square roots unravel intricate numerical mysteries. These concepts serve as beacons, guiding mathematical explorations into fractional territories. Proficiency in squares and square roots equips mathematicians to navigate varied mathematical landscapes, unveiling the elegance and complexity inherent within algebraic frameworks.
Square of 175
The square of 175 equals 30,625, obtained by multiplying 175 by itself, a fundamental operation in algebraic mathematics, uncovering inherent number properties.
Square Root of 175
The square root of 175 is approximately 13.228. This fundamental mathematical operation reveals the value that, when multiplied by itself, equals 175.
Square Root of 175: Approximately 13.228
Exponential Form: 175^½ or 175^0.5
Radical Form: √175
Is the Square Root of 175 Rational or Irrational?
Rational numbers are expressible as the quotient of two integers. Irrational numbers, however, cannot be represented as fractions of integers. Examples of irrational numbers include the square roots of non-perfect squares.
Methods to Find the Value of the Root 175
- Prime Factorization Method: Break down 175 into its prime factors. However, since 175 is not a perfect square, its prime factorization results in a mixture of prime factors.
- Long Division Method: Utilize the long division algorithm to approximate the square root of 175 iteratively.
- Using a Calculator: Most calculators are equipped with a square root function, enabling direct calculation of the square root of 175.
- Estimation: As 175 falls between the perfect squares of 169 (13 × 13) and 196 (14 × 14), an estimate can be made that its square root is likely between 13 and 14, closer to 13.
Square Root of 175 by Long Division Method:
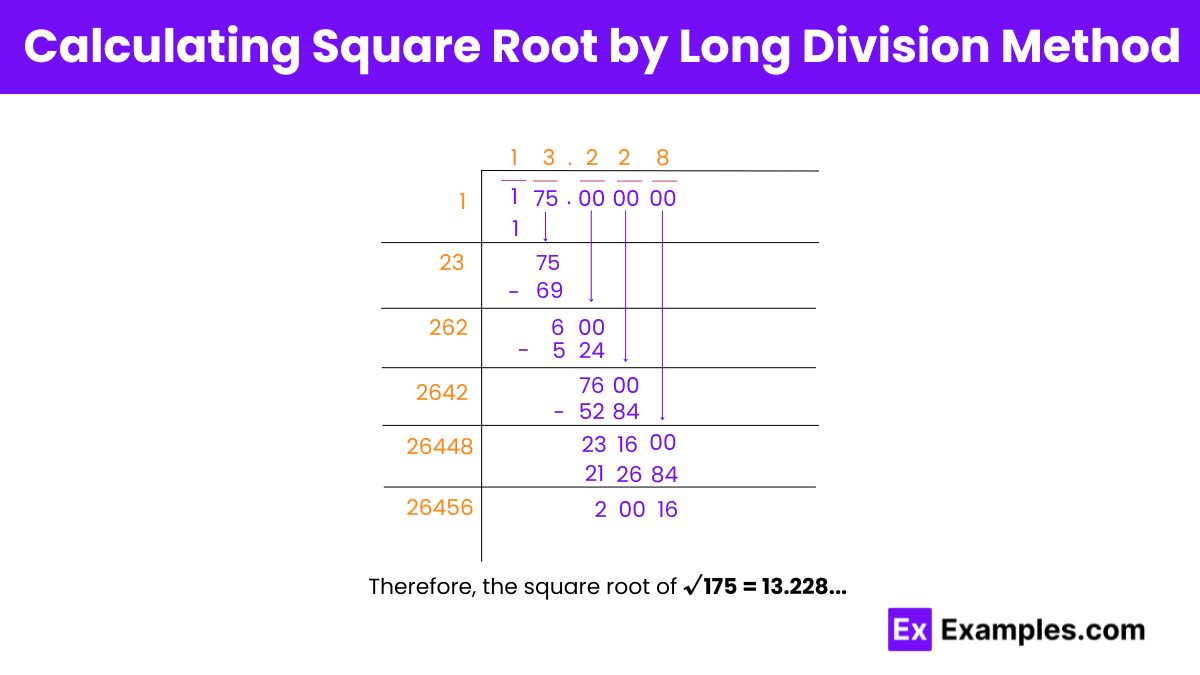
Step 1: Start pairing the digits from the right by placing a bar above them.
Step 2: Find a number whose square is less than or equal to 175. Using 23 as the divisor, the quotient is 13 and the remainder is 6.
Step 3: Double the divisor (23 × 2 = 46) and add a blank to its right. Guess a digit to fill the blank. Choose the largest digit that, when the new divisor is multiplied by the new quotient, gives a product less than or equal to the dividend. Divide and write the remainder. Repeat this process to obtain the desired decimal places.
Is 175 a Perfect Square or Not?
Perfect square cannot be expressed as the square of an integer. Therefore, the square root of 175 is an irrational number.
What is the prime factorization of 175?
The prime factorization of 175 is 5 × 5 × 7, where 5 and 7 are both prime numbers. Therefore, the prime factorization of 175 is 5² × 7.
What is the cube root of 175?
The cube root of 175 is approximately 5.495.
What is the value of √175 rounded to the nearest integer?
The square root of 175 rounded to the nearest integer is 13.
Share :
