Square & Square Root of 109
Square of 109
Hence, the square number of 109 is 11881. Mastering the process of squaring numbers is crucial in mathematics, especially in fields like algebra and geometry. It serves as a foundation for tackling more intricate problems and understanding advanced mathematical theories.
Square Root of 109
√109 = 10.4403065089
or
√109 = 10.440 up to three decimals
The square root of 109 is an irrational number, similar to the square roots of other non-perfect squares such as 24, because it cannot be exactly expressed as a fraction of two integers. Its approximate value is 10.4403065089. This value has importance in various mathematical fields, including geometry, where it can be used to determine the length of the side of a square that has an area of 109 square units. Furthermore, the square root of 109 is utilized in algebraic equations, engineering calculations, and physics formulas. It plays an essential role in understanding spatial relationships and achieving numerical approximations.
Exponential Form: 109^0.5 or 109¹/²
Radical Form: √109
Is the Square Root of 109 Rational or Irrational?
irrational number cannot be expressed as a simple fraction, where both the numerator and denominator are integers. The square root of 109, like that of most non-perfect squares, does not result in a whole number or a simple fraction, indicating its irrational nature. This characteristic is crucial in fields such as algebra and geometry, impacting calculations and theories involving square roots.
Rational numbers are those that can be expressed as a fraction with both the numerator and denominator being integers. This category includes a variety of numbers, such as simple fractions like 1/2, negative fractions like −3/4
Examples:4/3,3/5
Irrational numbers, in contrast, cannot be written as a simple fraction. This means there are no two integers that can form a fraction to express these numbers exactly. Irrational numbers have non-terminating, non-repeating decimal expansions. Many of them are found by taking the square root of numbers that aren’t perfect squares.
Examples:√3,√5
Methods to Find Value of Root 109
1. Using a Calculator
The simplest and most accurate method for most people is to use a calculator. By entering 109 and pressing the square root function, you can quickly obtain the value of √109.
2. Estimation
For an estimation without a calculator, you can find two perfect squares between which 109 falls (100 and 121, which are squares of 10 and 11, respectively). Since 109 is closer to 100, you can estimate √109 to be slightly under 10.5.
3. Newton’s Method (Numerical Approximation)
This method uses calculus and is very effective for finding more precise values of square roots. You start with a guess (x0, say 10) and use the formula:
xₙ₊₁ = 1/2(xₙ+109/xₙ)
Repeatedly apply this formula until the value stabilizes. This method converges very quickly to the actual square root.
4. Babylonian Method
Similar to Newton’s method, this ancient technique, also known as the “Hero’s method,” involves making a guess and refining it. It uses the same iterative formula as Newton’s method and is particularly useful when a high degree of accuracy is not required.
5. Long Division Method
This method is akin to traditional long division but adapted for square roots. It involves dividing the number into pairs of digits starting from the decimal point and subtracting squares of increasing digits until you get a result. This method can be cumbersome without practice but provides a step-by-step breakdown of the square root.
6. Using a Computer Algorithm
Programming languages such as Python, Java, or C++ can be used to calculate square roots to many decimal places using built-in functions or algorithms similar to the Newton’s method.
Square Root of 109 by Long Division Method
Step 1: Pairing the Digits
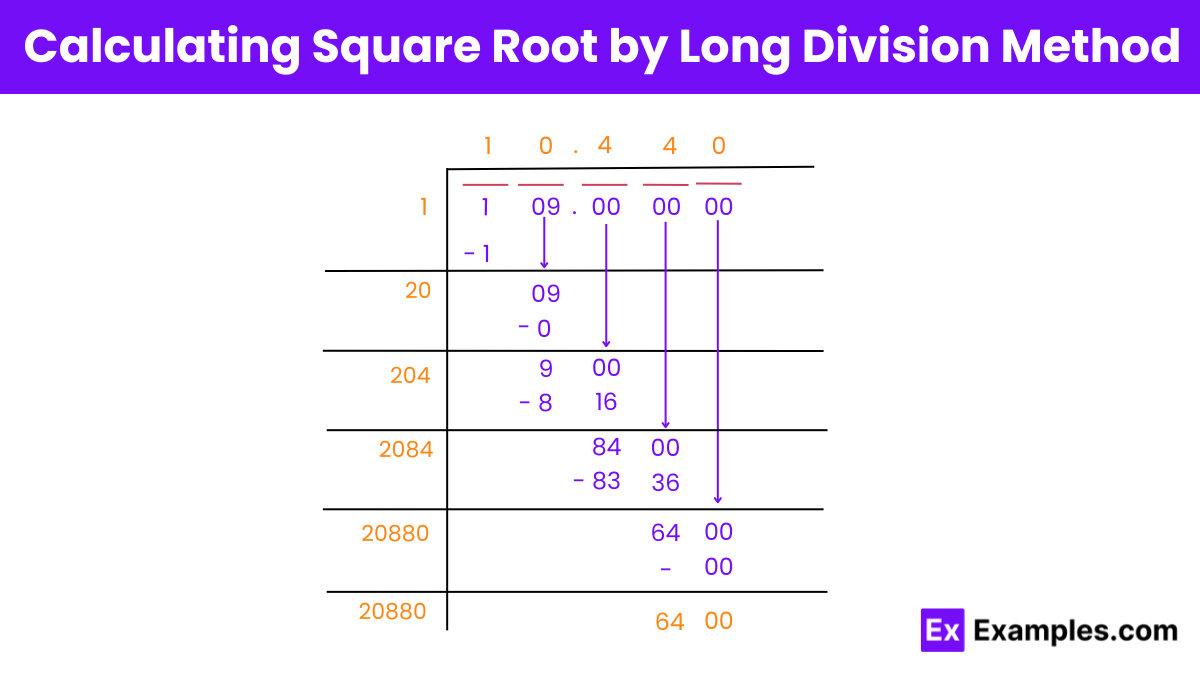
Start by pairing the digits of 109 from the right. This looks like: 1 | 09. Use a horizontal bar to show the pairing.
Step 2: Finding the Initial Quotient
Find a number which squared gives a result ≤ 1. Since 1 × 1 = 1, the first quotient digit is 1.
Step 3: Bringing Down the Next Pair
Bring down the next pair of digits (00) and double the current quotient (1) which gives 2. This 2 is the starting digit of our new divisor.
Step 4: Adding the Next Digit to the Divisor
Put a 0 in the one’s place of the new divisor to make 20, because 20 × 0 = 0. Subtract this from 9, bring down the next pair of zeros, and the new remainder is 900.
Step 5: Updating the Quotient
Now, multiply the current quotient (10) by 2 to get 20, which is the starting digit of the next divisor.
Step 6: Updating the Divisor Again
Place a 4 at the one’s place to make the new divisor 204, because 204 × 4 = 816. Subtract this from 900 to get 84, and bring down the next pair of zeros.
Step 7: Adjusting the Quotient
The quotient 104, when doubled, gives 208. This is the new starting digit of the divisor.
Step 8: Finalizing the Divisor
Again, place a 4 in the one’s place to get 2084. Multiplying 2084 by 4 gives 8336. Subtracting this from 8400, the new remainder is 64. Bring down the next pair of zeros.
Step 9: Adjusting the Quotient for the Final Steps
Double the latest quotient (1044) to get 2088, which is the starting digit of the next divisor.
Step 10: Completing the Calculation
Place a 0 at the one’s place of the new divisor (20880) because 20880 × 0 = 0. Subtract this from 6400 to get the final remainder of 6400.
Is 109 a Perfect Square root or Not?
A perfect square is a number that can be expressed as the square of an integer. For instance, numbers like 100 (10²) and 121 (11²) are perfect squares because they result from squaring whole numbers. However, 109 does not have an integer as its square root; the square root of 109 is approximately 10.44, which is not a whole number. Thus, 109 is not a perfect square.
FAQ’s
What is radical 109?
Refers to the square root of 109, which is an irrational number approximately equal to 10.44. It represents the non-integer root of the number 109.
What is the number 109?
The number 109 is a prime number, meaning it is greater than 1, has no positive divisors other than 1 and itself, and is an odd number.
Share :
