Square & Square Root of 11
Square of 11
To calculate the square of 11, you simply multiply 11 by itself:
Therefore, the square of 11 is 121. This straightforward calculation is a building block for more complex mathematical operations and concepts, including algebraic equations, geometric formulas, and statistical models.
Square Root of 11
Or
√11 = 3.316 up to three places of decimal.
The square root of √11, represented as 1111, is an irrational number, which means it can’t be accurately expressed as a fraction. The approximate value is 3.3166, positioning it between 3 and 4 on the number line. Being the square root of a non-perfect square, it does not resolve into a neat, whole number, embodying its irrational characteristic. This nature makes it an intriguing figure in both mathematical theory and practical computations.
Exponential Form of 11: (11)½ or or (11)0.5
Radical Form of 11: √11
Is the Square Root of 11 Rational or Irrational?
The square root of √11 is an irrational number.
When we delve into the nature of the square root of 11, we confront a fascinating aspect of numbers: the divide between rational and irrational numbers. To understand this distinction and determine the category of the square root of 11, let’s explore the definitions and characteristics of these two types of numbers.
Rational Numbers: These are numbers that can be expressed as the quotient or fraction qp of two integers, where p and q are integers and q is not zero. Examples include 1221, 4334, and −52−25. Rational numbers can also be represented as terminating or repeating decimals.
Irrational Numbers: In contrast, irrational numbers cannot be expressed as fractions or ratios of integers. They are non-repeating, non-terminating decimals without a predictable pattern. Famous examples include π, e, and the square root of 2 (22).
Now, let’s apply this knowledge to the square root of √11 (1111). To ascertain whether it is rational or irrational, we must determine if it can be represented as a fraction of two integers. Through mathematical proofs and properties, it is established that the square root of any non-perfect square (a number that is not an integer’s square like 1, 4, 9, 16, and so on) is always irrational. Since 11 is not a perfect square, its square root cannot be expressed as a simple fraction of integers.
Methods to Find Value of Root 11
Finding the value of mathematical expressions like the square root of a number involves various methods and techniques. Here are several approaches to finding the value of the square root of √11:
- Calculator: The simplest method is to use a calculator capable of calculating square roots. You can input “√11” into the calculator, and it will provide you with the approximate value of the square root of 11.
- Estimation: You can estimate the value of the square root of 11 by considering its proximity to other perfect square roots. Since 11 is between 9 (which has a square root of 3) and 16 (which has a square root of 4), you can estimate that √11 is slightly greater than 3 but less than 4.
- Long Division Method: The long division method involves finding the square root of a number through iterative calculations. While it’s more complex and time-consuming, it can provide a precise value. However, it’s not commonly used for manual calculations due to its complexity.
- Using Square Root Tables: Historically, square root tables were used to find the square roots of numbers. While they are less common today due to the prevalence of calculators, you can still find digital versions online or in mathematical reference books.
- Approximation Algorithms: There are various algorithms, such as the Newton-Raphson method, that can be used to approximate the value of square roots. These algorithms use iterative calculations to converge on increasingly accurate approximations of the square root.
- Graphical Representation: You can plot the graph of the function y = √x and locate the point corresponding to x = 11 on the x-axis. The value of y at this point will be the square root of 11.
- Using Binomial Expansion: Another method involves using the binomial expansion of (1 + x)^0.5 to approximate the square root of a number. While this method requires some mathematical proficiency, it can provide a relatively accurate approximation for the square root of 11.
By employing these methods, you can find the value of the square root of 11 with varying degrees of accuracy and complexity. Depending on your needs and the tools available, you can choose the method that best suits your requirements.
Square Root of 11 by Long Division Method
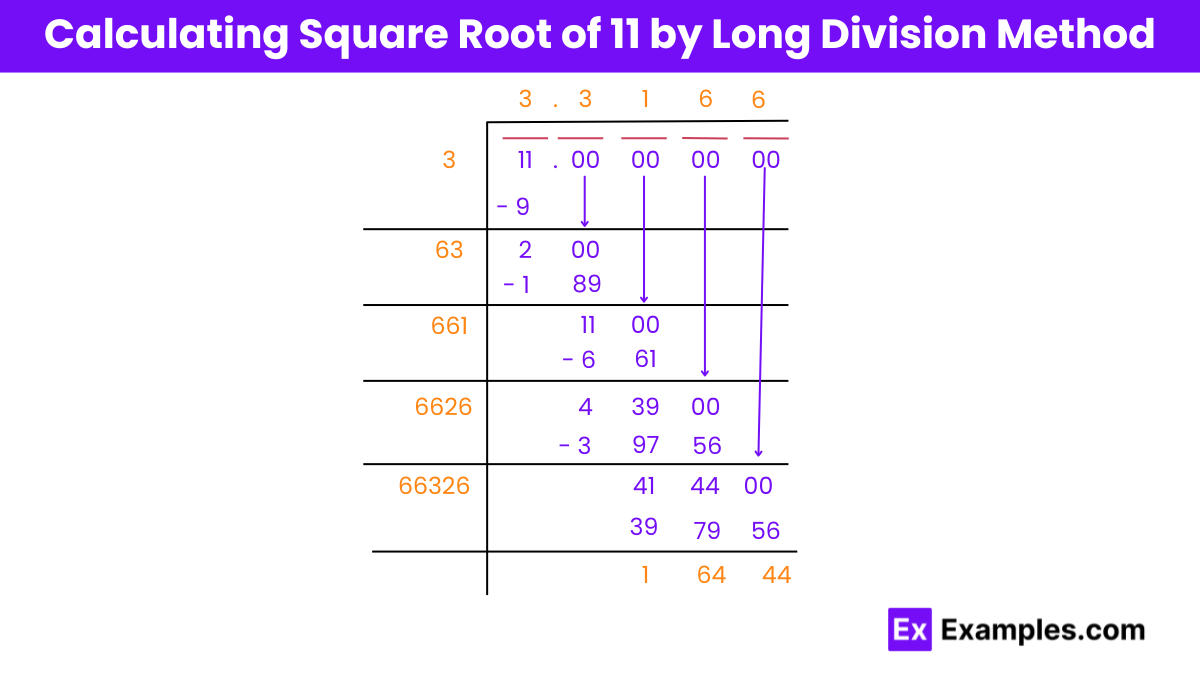
Finding the square root of √11 using the long division method involves a step-by-step process of approximation. Here’s how it’s done:
- Start by grouping the digits of 11 in pairs from the decimal point (if applicable). Since 11 is a whole number, there’s no need to add a decimal point.
- Find the largest integer whose square is less than or equal to 11. In this case, it’s 3, because 3^2 = 9.
- Subtract the square of 3 (which is 9) from 11, leaving a remainder of 2.
- Bring down the next pair of zeros (if any). Since 11 is a whole number, there are no additional digits to bring down.
- Double the quotient obtained so far (which is 3) and write it as the divisor. We get 6.
- Guess a digit to place in the quotient’s tenths place. We start with 0.
- Multiply the divisor (6) by the guessed digit (0), giving 60. Then, add another digit to make it as close to the dividend (2) as possible without exceeding it. The closest digit is 3, making the product 63.
- Subtract 63 from 200 (the remaining portion of the dividend), leaving a remainder of 137.
- Bring down the next pair of zeros (if any). Since 137 is less than 200, we can’t bring down any more digits.
- Double the quotient obtained so far (which is 30) and write it as the divisor. We get 60.
- Since we’ve already placed a digit in the tenths place of the quotient, we can continue the long division process by guessing digits for the hundredths place. We start with 0.
- Multiply the divisor (60) by the guessed digit (0), giving 0. Then, add another digit to make it as close to the remaining portion of the dividend (137) as possible without exceeding it. The closest digit is 2, making the product 120.
- Subtract 120 from 137, leaving a remainder of 17.
- Since the remainder is smaller than the divisor, we conclude the calculation.
So, the square root of 11, using the long division method, is approximately 3.31662479.
11 is Perfect Square root or Not
Yes, 11 is not a perfect square. A perfect square is a number that can be expressed as the product of an integer multiplied by itself. For example, 4 (2 * 2) and 9 (3 * 3) are perfect squares because they can be expressed as the square of an integer. However, 11 cannot be expressed as the product of an integer multiplied by itself, so it is not a perfect square. The square root of 11 is an irrational number, approximately equal to 3.31662479.
FAQS
1. What is the fastest way to find the square of a number?
A: The quickest method to square a number is to multiply it by itself. For instance, to find the square of 5, you would calculate 5×5=255×5=25.
2: Is the square root of 11 a perfect square?
A: No, the square root of 11 is not a perfect square. A perfect square is the product of an integer multiplied by itself, and 11 does not meet this criterion.
3: Is the square root of 11 a real number?
A: Yes, the square root of 11 is a real number. It is an irrational number that cannot be precisely expressed as a fraction or decimal, but it exists on the real number line.
4: Which number is closest to the square root of 11?
A: The number 3 is closest to the square root of 11. This is because 1111 is approximately 3.3166, making 3 the nearest whole number.
5: Is the square root of 11 a prime number?
A: No, the square root of 11 is not a prime number. Prime numbers are defined as whole numbers greater than 1 that have only two distinct positive divisors: 1 and themselves. The square root of 11, being an irrational number, does not meet these criteria.
In conclusion, squaring 11 yields 121, a straightforward process where 11 is multiplied by itself. On the other hand, the square root of 11, symbolized as 1111, is classified as an irrational number, indicating it cannot be precisely represented as a fraction or a finite or repeating decimal. It is situated between the integers 3 and 4 on the numerical continuum.
Share :
