Square & Square root of 111

Square of 111

111² (111 × 111) = 12321

the square number of 111 is 12321. This straightforward calculation serves as a foundation for more complex mathematical operations and concepts, such as algebraic equations, geometric formulas, and statistical models.

Square Root of 111

√111 = 10.5356537529

or

√111 = 10.535 up to three decimals

The square root of 111, denoted as √111, is approximately 10.5357. To find it, you look for the number which, when squared, equals 111. In mathematical terms, finding a square root is about identifying the number that raised to the power of 2 gives back the original number. You can visualize the square root of 111 as the side length of a square that covers an area of 111 square units. Understanding square roots is essential in various math fields and practical applications, such as geometry and algebra, and it’s helpful for calculating actual lengths or measurements from given area values.

Square Root of 111: 10.5356537529

Exponential Form: 111^1/2 or 111^0.5

Radical Form: √111

Is the Square Root of 111 Rational or Irrational?

The square root of 111 is an irrational number

This means that it cannot be expressed as a simple fraction where both the numerator and the denominator are integers. The decimal form of an irrational number goes on indefinitely without repeating, and this is the case with the square root of 111. Since 111 is not a perfect square (meaning there’s no integer that can be squared to produce 111), its square root cannot be represented as a precise fraction and thus is irrational.

Rational numbers are numbers that you can write as a fraction, with both the top number (numerator) and the bottom number (denominator) being whole numbers. This group includes regular fractions like 1/2, negative fractions like -3/4, whole numbers like 5 (since you can write it as 5/1), and even zero.

Examples: 5/3, -5/2

Irrational numbers, on the other hand, are numbers that you can’t write as a simple fraction. Their decimal forms go on forever without repeating any pattern. These usually include the square roots of numbers that aren’t perfect squares.

Examples: √2, √3,

Methods to Find Value of Root 111

1. Calculator Method:
   • This is the simplest and most accurate way for most practical purposes. Simply enter √111 into a calculator to get an approximate decimal value.
2. Estimation:
   • You can estimate the square root by recognizing that it lies between the square roots of 100 (which is 10) and 121 (which is 11). Thus, √111 is slightly above 10.5.
3. Newton’s Method (Numerical approximation):
   • This method uses calculus to approximate roots and can be very precise. Start with an initial guess (like 10.5) and use the formula :xₙₑᵥᵥ=xₒₗₔ​−f(xₒₗₔ​​)/f′(xₒₗₔ​​)​where f(x)=x²−111. This formula iteratively refines the guess based on the function and its derivative.
4. Babylonian Method (or Heron’s Method):
   • This is an ancient algorithm for finding square roots that is a special case of Newton’s Method :xₙₑᵥᵥ= 2/1(xₒₗₔ + 111/xₒₗₔ)Start with an initial guess (like 10.5) and repeatedly apply this formula until the changes become negligible, which typically happens very quickly.
5. Using a Computer or Spreadsheet:
   • If you are using a computer or a spreadsheet like Excel, you can simply use the square root function provided (usually SQRT() or something similar) and input 111 to get the result.

These methods range from very simple and less precise (estimation) to more complex but highly accurate (Newton’s Method). The choice of method depends on your specific needs and available resources.

Square Root of 111 by Long Division Method

1. Find Y: Look for a number Y such that Y² ≤ 1. The number 1 works because 1² = 1.
2. Divide: Divide 01 by 1. The quotient is 1 and the remainder is 0.
3. Bring down the next pair: Now consider the next pair, 11. This makes your new dividend 11.
4. Update the divisor: Add the last digit of the quotient (1) to the divisor (1), which gives you 2. Find a digit Z such that 20Z ≤ 11. Z is 0 here, making the new divisor 20.
5. Divide again: Divide 11 by 20. The quotient is 0 and the remainder is 11 – 0 = 11.
6. Next steps for decimal places:
   • Bring down 00 to make the new dividend 1100.
   • Add the last digit of the quotient (0) to the divisor (20), resulting in 20 again.
   • Find a digit Z such that 205Z ≤ 1100. Z is 5, so the new divisor is 205.
   • Divide 1100 by 205. The quotient is 5, and the remainder is 1100 – 1025 = 75.
   • You can continue to bring down more zeros and repeat the steps to find more decimal places.

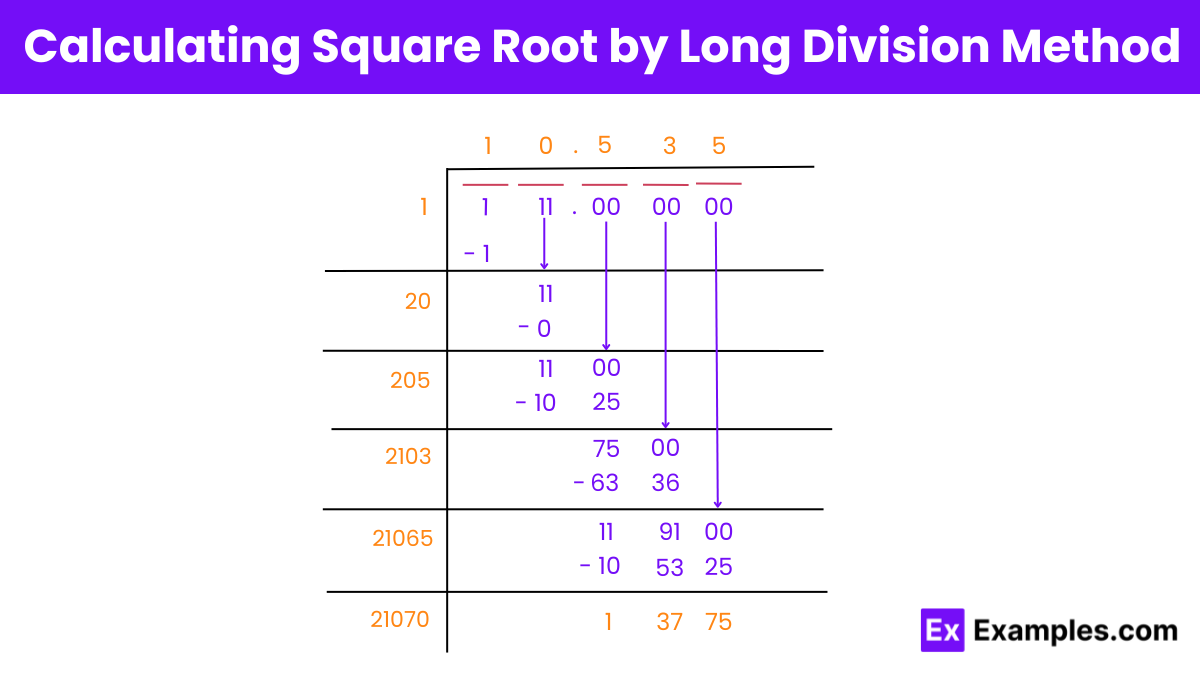
By this method, the approximate square root of 111 is 10.5.

Is 111 Perfect Square root or Not

The number 111 is not a perfect square

A perfect square is an integer that is the square of another integer. For example, 121 is a perfect square because it is 11 squared (11 x 11 = 121). Since there is no integer that when squared gives 111, it cannot be a perfect square. The square root of 111 is an irrational number, approximately 10.5357, further confirming that it is not a perfect square.

FAQ’S

Which number is closest to √ 111?

The number closest to the square root of 111 is 11. This is because √111 is approximately 10.5357, and the nearest whole number is 11.

What can 111 be divided by?

The number 111 can be divided by 1, 3, 37, and 111. These numbers are the divisors of 111, meaning they divide it without leaving a remainder.

What numbers can make 111?

Various pairs of numbers can be added together to make 111, such as 110 + 1, 100 + 11, 55 + 56, and so forth. In terms of multiplication, 3 × 37 = 111.

Why 111 is not prime?

The number 111 is not prime because it has divisors other than 1 and itself. A prime number has exactly two distinct positive divisors: 1 and the number itself. For 111, it can be divided by 1, 3, 37, and 111. Therefore, since it has more than two divisors, it is not a prime number.