Square & Square Root of 112

Square of 112

112² (112 × 112) = 12544

The square number of 112 is 12544. This simple calculation forms the basis for more advanced mathematical operations and concepts, such as algebraic equations, geometric formulas, and statistical models.

Square Root of 112

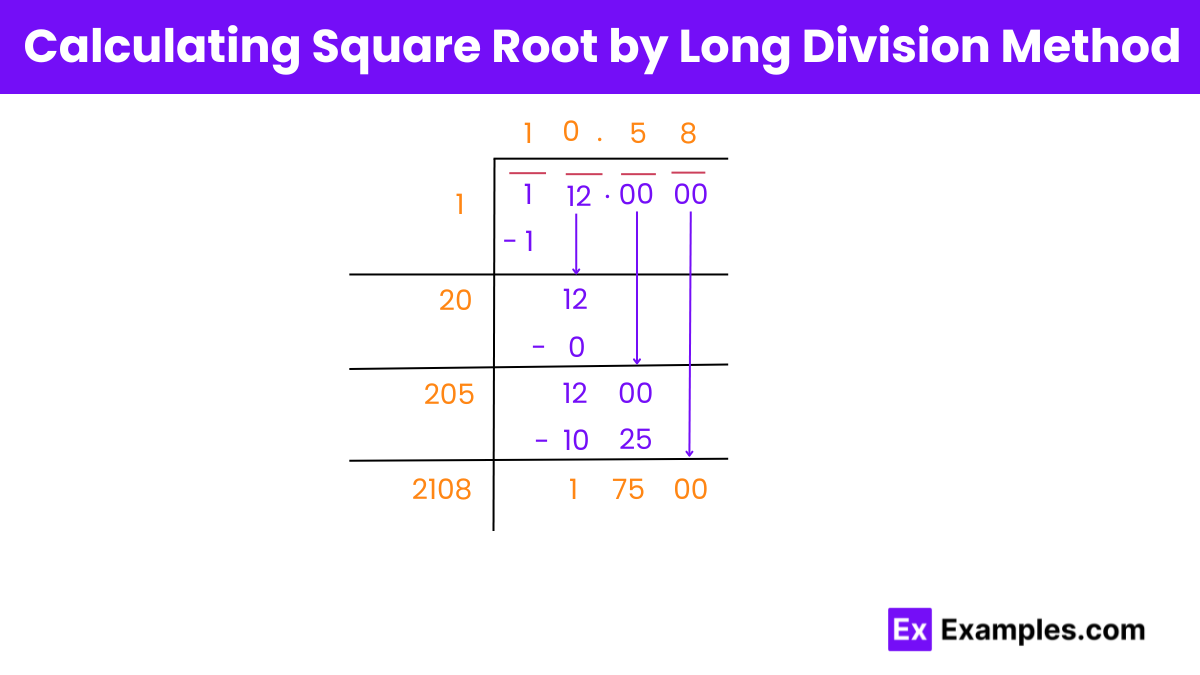
√112 = 10.5830052443

or

√112 = 10.583 up to three decimals

The square root of 112, denoted as √112, is approximately 10.5830. To find it, you search for the number which, when squared, equals 112. Essentially, finding a square root means identifying the number that, when raised to the power of 2, results in the original number. You can think of the square root of 112 as the length of a side of a square that has an area of 112 square units. Understanding square roots is crucial in various areas of mathematics and practical scenarios, such as geometry and algebra, where it helps calculate the actual lengths or measurements from given area values.

Square Root of 112: 10.5830052443

Exponential Form: 112^1/2 or 112^0.5

Radical Form: √112

Is the Square Root of 112 Rational or Irrational?

The square root of 112 is an irrational number

A number is considered irrational if it cannot be expressed as a simple fraction, where both the numerator and the denominator are integers. In the case of √112, this number can’t be simplified into a fraction because 112 is not a perfect square. Instead, it is expressed as a non-repeating, non-terminating decimal.

A rational number can be expressed as a fraction where both the numerator and the denominator are integers, and the denominator is not zero.

Examples: 2/1​, 4/5, and −7/3​.

An irrational number cannot be expressed as a simple fraction where both the numerator and denominator are integers. These numbers have non-repeating, non-terminating decimal expansions.

Examples: √2, π, and e.

Methods to Find Value of Root 112

1. Calculator Method: The simplest way is to use a calculator. Just type in “112” followed by the square root function.
2. Estimation: You can estimate √112 by noting that √100 = 10 and √121 = 11, so √112 should be slightly more than 10.5.
3. Babylonian Method (or Iterative Guess and Check):
   • Guess a number that might be the square root.
   • Compute the average of the guess and the result of dividing your number (112) by that guess.
   • Use this average as a new guess and repeat until the guess is close enough to the actual square root.
4. Newton’s Method:
   • Choose an initial guess for the root.
   • Apply the formula x ₓ₊ₙ=ₓₙ −f(xₙ )/f′(xₙ )where f(x) = x² − 112.
   • Repeat using the result as the new guess until the value converges to a stable number.
5. Exponential and Logarithmic Functions:
   • Use logarithms to transform the square root into an exponent, 112​=10log₁₀​⁽¹¹²⁾/².
   • Calculate using a scientific calculator or logarithmic tables.

Square Root of 112 by Long Division Method

1. Pair the Digits: Start by pairing the digits of 112 from right to left, placing a bar over each pair. Since 112 has three digits, pair the last two digits together as ’12’ and the first digit ‘1’ alone. If there are decimals, pair the zeros in groups of two from the decimal point rightwards.
2. First Division: Look for a number that, when squared, gives a product less than or equal to the first pair or single digit. For ‘1’, the number is 1. Write ‘1’ as the first digit of the quotient. Subtract 1 squared (1) from 1, resulting in a remainder of 0.
3. Bring Down Next Pair: Drag down the next pair (’12’) next to the remainder, making it ‘012’. Double the divisor (1 becomes 2) and write it below.
4. Second Division: Find a number (X) such that ‘2X’ times ‘X’ is less than or equal to ‘012’. The number is 0, so add ‘0’ next to the quotient beside ‘1’ and also next to ‘2’ in the divisor, making the divisor 20.
5. Continue Process: Subtract and bring down the next pair of zeros from any decimal part. Repeat the process to refine the quotient to the desired number of decimal places, each time doubling the part of the divisor before the last digit and finding the new digit of the quotient that maximizes the product without exceeding the new number formed by the remainder.

Is 112 Perfect Square root or Not

112 is not a perfect square

No, A perfect square is a number that can be expressed as the square of an integer. For example, 121 is a perfect square because it is 11×11. In the case of 112, there is no integer that, when squared, equals 112. The square root of 112 is an irrational number, approximately 10.583, which confirms that it is not a perfect square.

FAQ’S

What is the square factorization of 112?

To perform the square factorization of 112, we need to factor it down to its prime components and organize them into squares. The prime factorization of 112 is 2⁴×7.

What is the closest perfect square to 112?

The closest perfect squares to 112 are 121 (which is 11²) and 100 (which is 10²). The number 121 is closer to 112 than 100.

What are multiples of 112?

The multiples of 112 are obtained by multiplying 112 by integers. The first few multiples are 112, 224, 336, 448, 560, etc.

What are prime factors of 112?

The prime factors of 112 are 2 and 7. This is because 112 can be factored into 2⁴×7, where 2 and 7 are both prime numbers.