Square & Square root of 116
Square of 116
The square of 116, denoted as 116^2, equals 13,456. To compute it, you multiply 116 by itself, resulting in 13,456. In mathematical terms, squaring a number means raising it to the power of 2. Visually, you can represent the square of 116 as a square with sides of length 116 units, where the area of the square is 13,456 square units. Understanding squares and their values is fundamental in various mathematical concepts and applications, such as geometry, algebra, and calculating areas or volumes. In real-world scenarios, knowing the square of 116 aids in calculations involving quantities or measurements squared.
Square Root of 116
The square root of 116, denoted as √116, is approximately 10.77. In mathematics, the square root of a number is a value that, when multiplied by itself, gives the original number. So, for 116, the square root is approximately 10.77 because 10.77 multiplied by itself equals approximately 116. This can also be represented as √116 ≈ 10.77. Understanding square roots is essential in various mathematical calculations, such as finding the side length of a square with a given area or solving quadratic equations. In real-world scenarios, square roots are commonly used in fields like engineering, physics, and finance.
Exponential Form: 116^1/2 or 116^0.5
Radical Form: √116
Is the Square Root of 116 Rational or Irrational?
This is because 116 is not a perfect square, meaning it cannot be expressed as the square of any integer. In general, the square root of any non-perfect square is irrational, which implies it cannot be represented as a simple fraction, and its decimal representation does not terminate or repeat.
Methods to Find Value of Root 116
To find the value of the square root of 116, you can use several methods, depending on the tools available and the precision required. Here are some common methods:
Estimation:
- Start by identifying two perfect squares between which 116 lies (e.g., 100 and 121, whose square roots are 10 and 11, respectively).
- Estimate that √116 is between 10 and 11. Further refine your estimate by considering how close 116 is to these perfect squares.
Long Division Method:
- This traditional method involves dividing the number into pairs of digits starting from the decimal point and finding the largest square number less than or equal to each pair.
- This method can be tedious but yields a very precise decimal value of the square root.
Calculator:
- The simplest and most accurate method for most practical purposes is to use a scientific calculator or calculator software, which can compute the square root directly.
Square Root of 116 by Long Division Method
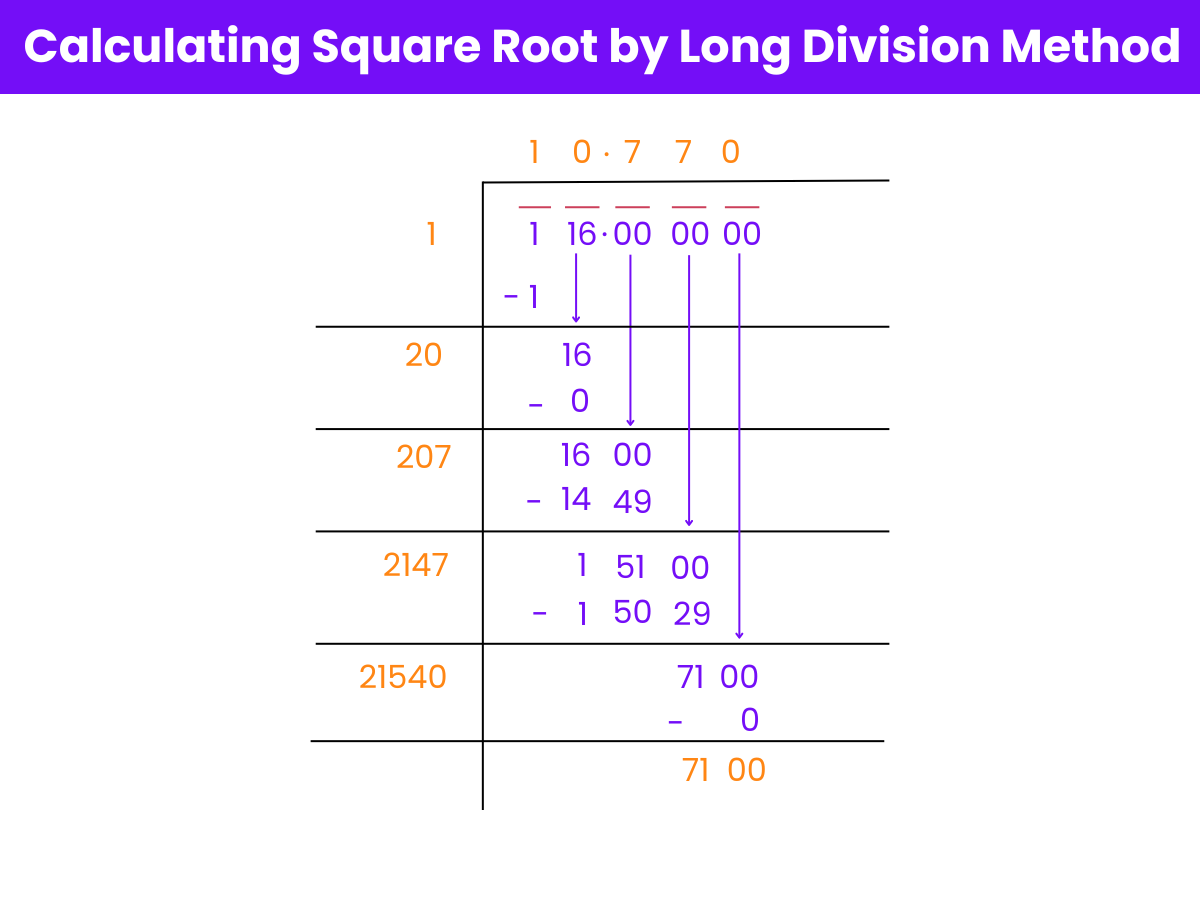
To find the square root of 116 using the long division method, follow these simplified steps:
Step 1: Pair the digits and start the division.
- Write down 116 as 116.000000, taking digits in pairs from the right. The number 1 stands alone.
- Divide 1 by a number that, when squared, gives ≤1. This number is 1, leaving a quotient of 1 and remainder 0.
- Double the quotient to get 2. The new divisor begins with 20. Bring down the next pair, 16.
Step 2: Continue the division with larger divisors.
- Seek a digit that, added to 20 and then multiplied by itself, stays under or equal to 16. Since no single digit fits, bring down two zeros, making the dividend 1600.
- With 10 as the current quotient, double it to get 200 as part of the next potential divisor. Adding 7 to 200 and multiplying by 7 results in 1449, fitting under 1600.
Step 3: Refine the quotient and finish the calculation.
- The quotient now is 10.7, with a remainder of 151. Bring down the next pair of zeros, making 15100 the new dividend.
- Doubling 10.7 for a new divisor base gives 214. Thus, the new divisor starts at 2140. Adding 7 and multiplying by 2147 results in 15029, subtracted from 15100, leaves a small remainder.
- Continue this process, refining the quotient to increase precision until achieving the desired accuracy, around three decimal places.
The approximate square root of 116 by this method is 10.770, calculated through repetitive approximation and refinement.
116 is Perfect Square root or Not
A perfect square is a number that can be expressed as the square of an integer. Since the square root of 116 is approximately 10.77, which is not an integer, 116 cannot be expressed as the square of any integer. Thus, it is not a perfect square.
FAQ’S
What are the factors of 116?
The factors of 116 are the numbers that divide it evenly. These factors are 1, 2, 4, 29, 58, and 116.
What are the multiples of 116?
The multiples of 116 are numbers obtained by multiplying 116 by integers. Some examples are 116, 232, 348, 464, 580, and so on, increasing by increments of 116.
What are the prime factors 116?
The prime factors of 116 are the prime numbers that multiply together to give 116. These prime factors are 2 and 29, with 2 being repeated twice.
Share :
