Square & Square Root of 120
Square of 120
The squares of a number refers to the result of multiplying the number by itself. When calculating the square of 120, you multiply 120 by 120.
Calculation:
Therefore, the square of 120 is 14,400. This calculation is used frequently in various mathematical contexts, including algebra, geometry, and in practical real-world applications where area or power calculations are necessary.
Square Root of 120
√120 = 10.9544511501
or
√120 = 10.954
Thus, the square root of 120 is approximately 10.95. This calculation is crucial in various mathematical and practical contexts, such as geometry, where it might represent the side length of a square whose area is close to 120 square units. It’s also significant in fields like algebra and engineering, where understanding square roots is essential for solving problems involving areas and other applications that require precise measurements.
Square Root of 120: 10.95
Exponential Form: 120^½ or 120^0.5
Radical Form: √120
Is the Square Root of 120 Rational or Irrational?
Here’s a simple way to understand this: A rational number is any number that you can write as a fraction where both the numerator (top number) and the denominator (bottom number) are whole numbers. An irrational number, on the other hand, cannot be written this way because it has a decimal that goes on forever without repeating.
For the square root of a number to be rational, that number must be a perfect square (like 4, 9, 16, etc., where the square roots are 2, 3, 4, respectively). Since 120 is not a perfect square—meaning no whole number multiplied by itself gives exactly 120—its square root does not result in a whole number or a simple fraction. Therefore, the square root of 120, which is about 10.95, is an irrational number with a decimal that never ends or repeats.
Methods to Find Value of Root 120
Using a Calculator
The simplest and most accurate way to find the square root of 120 is by using a calculator. Just enter 120 followed by the square root function, and you will get an immediate and precise result.
Estimation
If you don’t have a calculator handy, you can estimate the square root of 120 by identifying perfect squares that are close to 120. For example:
- The square root of 121 (a perfect square) is 11.
- The square root of 100 (another perfect square) is 10.
- Since 120 is between 100 and 121, its square root will be slightly more than 10 but less than 11. A rough estimate would place it around 10.95.
Long Division Method
The long division method is a manual technique that involves using a process similar to traditional long division to arrive at a more precise value of the square root:
- Divide the number into pairs of digits starting from the decimal point.
- Find the largest square less than or equal to the first pair or single digit, subtract it, bring down the next pair of digits, and continue the process.
Repeated Subtraction Method
This is a more intuitive method for finding square roots, particularly useful for teaching basic concepts of square roots to beginners. It involves repeatedly subtracting odd numbers from the number for which the square root is sought (in this case, 120) until you reach zero. The number of times you can perform this subtraction corresponds to the square root of the original number. However, this method is more practical for smaller numbers or perfect squares.
Square Root of 120 by Long Division Method
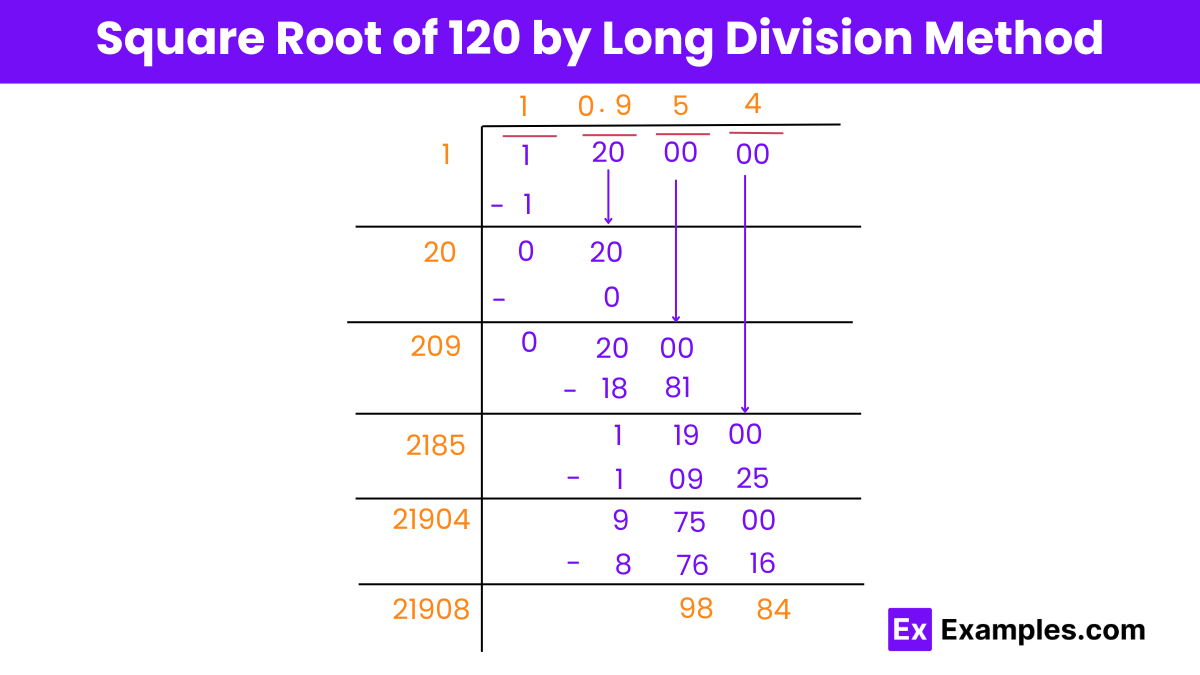
Step 1: Pair the Digits
Starting from the right, pair up the digits of the number by placing a bar above them. If there’s an odd number of digits, the leftmost pair may consist of a single digit.
Step 2: Determine the First Quotient
Identify a number whose square is less than or equal to the first pair. In your example, the first pair is ‘1’. Since the square of 1 is 1, which is not greater than 1, your first quotient digit is 1. Subtract the square of this number from the first pair, and bring down the next pair (if available) to form a new number. the next pair is added as the divisor, i.e. 20
Step 3: Update the Divisor
Double the current quotient. This doubled number is used as the base of your new divisor. You then find the largest single digit which, when added to this new divisor and multiplied by the same digit, results in a product that is less than or equal to the current dividend formed by the subtraction in Step 2 and the next pair brought down.
Step 4: Repeat the Process
Continue the process by updating the dividend (subtracting the last product from the current dividend and bringing down the next pair of digits), doubling the current quotient for the new base of the divisor, and finding the next digit of the quotient as described in Step 3.
Step 5: Finalize the Quotient
Continue repeating the process until all pairs of digits have been brought down and used up. The quotient obtained through this method is the square root of the original number, or the result of the division if you are dividing.
Step 6: Completion
The process is repeated until there are no more digits to bring down. The final quotient obtained is the answer to your initial mathematical problem.
120 is Perfect Square Root or Not
A perfect square is a number that can be expressed as the square of an integer. For a number to be a perfect square, there should be an integer 𝑛 such that 𝑛 ×𝑛 =number.
For example, 121 is a perfect square because it can be expressed as 11×11. However, when you try to find integers whose square gives 120, you won’t find any, because the squares of 10 and 11 are 100 and 121, respectively, neither of which is 120.
Therefore, since there is no integer whose square equals 120, it is not a perfect square.
FAQ’s
What is the simplified form of √ 120?
The simplified form of √120 is 2√30 This is obtained by factoring 120 into 4 × 30 and taking the square root of 4 out as 2.
What is the nearest whole number to the square root of 120?
The nearest whole number to the square root of 120 is 11. The square root of 120 is approximately 10.95, which rounds up to 11.
Share :
