Square & Square Root of 125 – Methods, Calculation, Formula, How to find

Square of 125

The square number of 125 is the result when you multiply 125 by itself. In mathematical terms, it’s represented as 125² or 125×125. When you calculate it, the square of 125 equals 15,625.

Square Root of 125

The square root of 125 is approximately 11.180. This is an irrational number, meaning it cannot be expressed as a simple fraction, and its decimal representation goes on indefinitely without repeating.

Is the Square Root of 125 Rational or Irrational?

To understand why, let’s break it down:

An irrational number is a number that cannot be expressed as a simple fraction (i.e., the ratio of two integers) and whose decimal representation goes on infinitely without repeating. When we try to find the square root of 125, we find that it doesn’t simplify to a whole number or a fraction. The approximate value of the square root of 125 is around 11.1803. This decimal goes on infinitely without repeating any pattern.

Therefore, because the square root of 125 cannot be expressed as a fraction and its decimal representation is non-repeating and non-terminating, it is considered an irrational number.

Rational numbers are numbers that can be expressed as a fraction, where both the numerator and the denominator are integers, and the denominator is not zero.

Examples: 3/4,5/1

Irrational numbers are numbers that cannot be expressed as a simple fraction, with decimal expansions that are non-terminating and non-repeating. These numbers often arise in geometry and algebra, especially involving roots of numbers that are not perfect squares or certain ratios like the circumference to the diameter of a circle (π).

Examples: √22​ and π.

Methods to Find Value of Root 125

Estimation:

You can start by identifying perfect squares that are close to 125, such as 121 (11² ) and 144 (12²).
Estimate that the square root of 125 is slightly more than 11, as 125 is slightly more than 121.
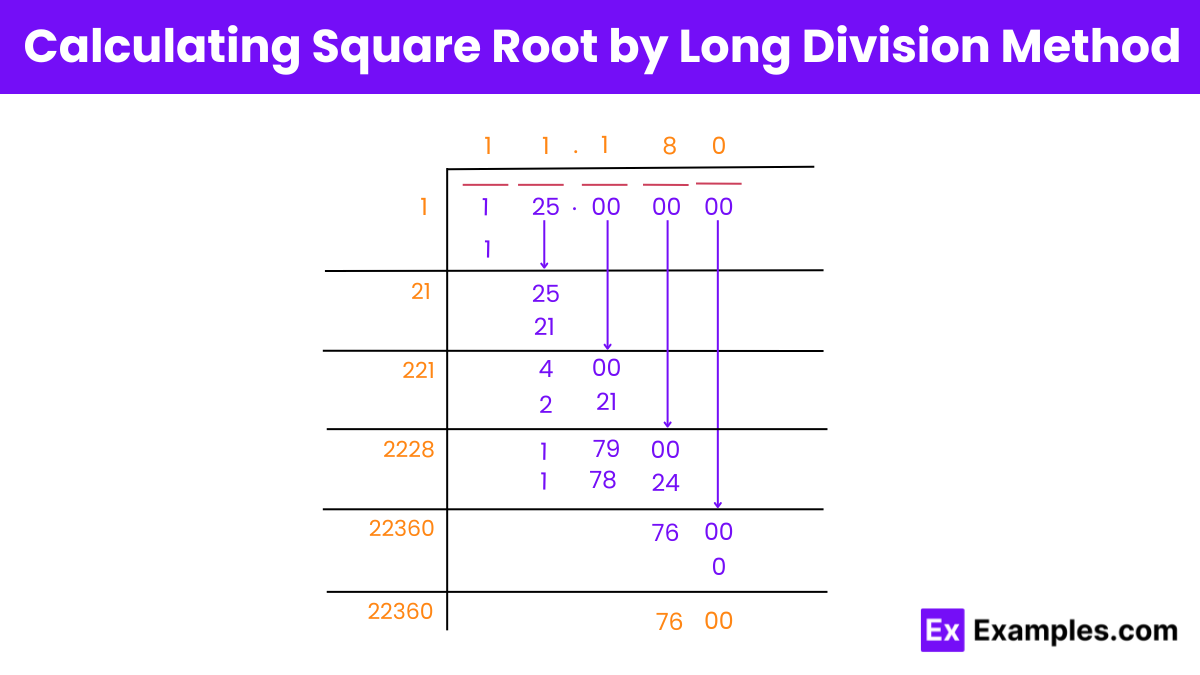
Long Division Method:

This traditional method involves a step-by-step procedure similar to long division. It helps find more precise values of square roots manually.
Calculator:

The simplest and most accurate way to find the square root of any number is using a calculator. Simply entering “√125” will give the precise value quickly.
Newton’s Method (or Newton-Raphson Method):

This is an iterative numerical method used for finding approximations to the roots (or zeroes) of a real-valued function. For √125 , the function would be f(x)=x²−125.
Start with an initial guess, say x₀=11, and iterate using the formula:
xₙ₊₁ =xₙ − xₙ² − 125/2xₙ
f(x)x² − 125 and its derivative f′(x)=2x.

Square Root of 125 by Long Division Method

1. Pair the Digits: Start from the right and pair the digits. For 125, create the pairs 1 and 25.
2. Find the Largest Square: Divide the left-most pair (1) by the largest number whose square is less than or equal to it. In this case, the largest number is 1.
3. Update the Divisor: Double the divisor from the previous step (making it 2) and write it with a space on its right. Guess the largest digit to fill this space that forms a new divisor. This digit also becomes part of the quotient. Multiply the new divisor by the new quotient digit to get a product that is less than or equal to the pair of digits being considered. Subtract this product from the pair to find the remainder.
4. Repeat for Precision: Continue this process, bringing down pairs of zeros if necessary, to calculate more decimal places of the square root.

Is 125 Perfect Square root or Not

No, A perfect square is a number that can be expressed as the square of an integer. The closest perfect squares to 125 are 121 (11²) and 144 (12²), and since there’s no integer whose square equals 125, it is not a perfect square.

FAQ’S

What is the square of 125 in Vedic math’s?

In Vedic Mathematics, squaring numbers close to base values like 10, 100, etc., can be done quite efficiently. Here’s a simpler breakdown for squaring 125 using Vedic math techniques:

1. Difference from Base: Determine how much the number exceeds the base. For 125 and base 100, the difference is +25.
2. Square the Difference: Square the excess, so 252=625.
3. Sum of the Number and the Excess: Add the excess to the original number. 125+25=150.
4. Multiply the Sum by the Base: Multiply the result from the previous step by the base (100). 150×100=15000.
5. Add the Results: Add the squared difference to the multiplication result. 15000+625=15625.

What is a cube root of 125?

The cube root of 125 is 5. This means that 5×5×5=125. The number 125 is a perfect cube because it can be expressed as the cube of an integer.