Square & Square Root of 144
Square & Square Root of 144
Square 144
The square of 144 represents the result when the number 144 is multiplied by itself.
In mathematical notation, this is expressed as 144². To determine the square of 144, you simply perform the multiplication of 144 by 144.
144² (144 × 144) = 20,736
This calculation involves straightforward arithmetic, requiring the multiplication of 144 by itself. It is a common operation found in various mathematical fields, particularly in geometry where squaring numbers can be related to determining areas, and in algebra where exponentiation plays a key role in solving equations and exploring numeric properties.
Square Root of 144
The square root of 144 refers to the number that, when multiplied by itself, yields the product 144. In mathematical terms, finding the square root is the inverse operation of squaring. The notation for the square root of 144 is √144.
To calculate the square root of 144, you identify the number that produces 144 when squared. The calculation reveals that 12 × 12 = 144, indicating that 12 is the square root of 144.
Calculating the square root of 144 is a straightforward process because 144 is a perfect square. Perfect squares are numbers that result from squaring whole numbers. Hence, the square root of 144 is 12, which demonstrates a basic arithmetic principle used frequently in mathematics, especially in operations involving root extraction and square function assessments.
Square Root of 144: 12
Exponential Form: 144^½ or 144^0.5
Radical Form: √144
Is the Square Root of 144 Rational or Irrational?
The square root of 144 is an rational number
To understand whether the square root of 144 is rational or irrational, let’s first define these terms.
Rational numbers are those expressible as a fraction of two integers, where the denominator is not zero, written as a/b.
Examples include 1/2, -3, and 5.
Irrational numbers, however, cannot be expressed as simple fractions of two integers. Their decimal representations are non-repeating and non-terminating.
Examples include √2, π (pi), and √3.
Square Root of 144 as Rational:
When we calculate the square root of 144, we find that it simplifies to the rational number 12. This is because 12 can be expressed as the fraction 12/1, where both 12 and 1 are integers, and the denominator is not zero. Additionally, the decimal expansion of the square root of 144 terminates after a finite number of digits, indicating its rational nature.
In summary, the square root of 144 is rational because it simplifies to a rational number (12) when calculated, and its decimal expansion terminates.
Method to Find Value of Root 144
There are several methods to calculate the square root of 144, each varying in approach and complexity. Understanding these methods can help in different mathematical contexts, particularly in education, where various strategies are taught to develop a deeper understanding of arithmetic operations.
1. Guess and Check Method
his is a simple method where you guess potential numbers that might be the square root of 144 and check by squaring them. It’s straightforward and effective for perfect squares. For instance, squaring 12 confirms that 12² = 144, thus 12 is the square root.
2. Prime Factorization Method
This involves breaking down 144 into its prime factors. The prime factorization of 144 is 2⁴× 3² . The square root is then calculated by taking half the power of each prime factor: 2⁴/²× 3²/² = 2² × 3 = 4 × 3 = 12.
3. Long Division Method
This traditional method involves a step-by-step approach similar to long division. It’s particularly useful for finding the square roots of non-perfect squares or when higher precision is needed. For perfect squares like 144, it clearly shows that the square root is 12.
4. Using a Calculator
For quick results, using a calculator is the most straightforward method. You simply enter 144 and press the square root function to get the result.
Each method serves a different need-some are more educational, while others are about efficiency. Understanding these methods not only aids in calculating the square root of 144 but also enhances general mathematical skills and knowledge.
Square Root of 144 by Prime Factorization Method
The prime factorization method to find the square root of 144 involves breaking down the number 144 into its basic prime factors. Prime factorization means expressing a number as the product of its prime numbers, which are numbers greater than 1 that have no divisors other than 1 and themselves.
Here’s how to use the prime factorization method for 144:
- Divide the Number: Start by dividing 144 by the smallest prime number that can evenly divide it, which is 2. Keep dividing the quotient by 2 until you cannot evenly divide by 2 anymore.
- 144 ÷ 2 = 72
- 72 ÷ 2 = 36
- 36 ÷ 2 = 18
- 18 ÷ 2 = 9
- Now, 9 is not divisible by 2, so we switch to the next smallest prime number, which is 3.
- 9 ÷ 3 = 3
- 3 ÷ 3 = 1
- Write Down the Prime Factors: The prime factors of 144, based on the divisions above, are 2⁴ and 3².
- Calculate the Square Root: To find the square root, take the square root of each prime factor and multiply them. For each prime factor, divide the exponent by 2 and multiply the results.
√144 = √(2⁴× 3²) = 2⁴/²× 3²/² = 2² × 3 = 4 × 3 = 12.
Therefore, the square root of 144 by the prime factorization method is 12. This method is not only useful for finding square roots but also helps in understanding the fundamental structure of numbers, enhancing one’s ability to perform various mathematical calculations.
Square Root of 144 by Long Division Method
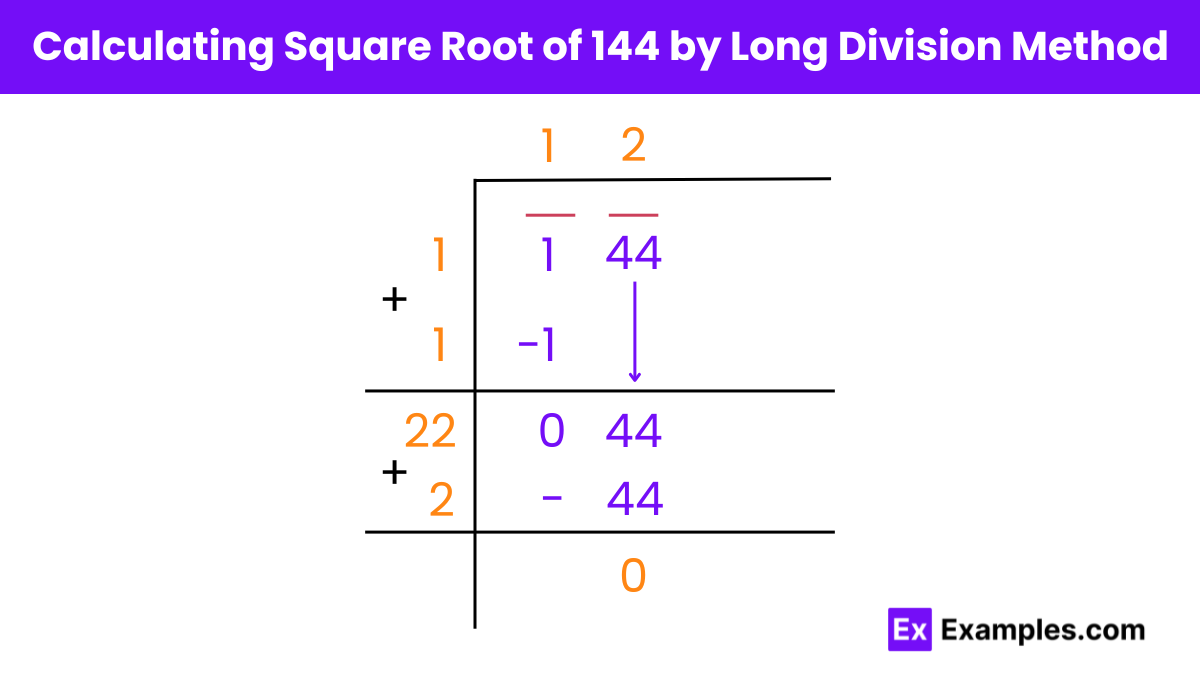
The long division method is a systematic approach to finding the square root of a number, particularly useful when dealing with perfect squares like 144. Here’s how to apply this method to calculate the square root of 144 step-by-step:
Step 1: Set Up the Number
Arrange 144 for the division, and start by grouping the digits in pairs from the right. For 144, place a bar over the pair of digits from the right and the remaining single digit on the left. This means you put one bar over 44 and another bar over the 1.
Step 2: Find the First Digit
Identify a number which, when squared, gives a result equal to or less than the first group under the bar, here ‘1’. The highest square less than or equal to 1 is 1 (since 1² = 1).
Step 3: Bring Down the Next Pair
Now, bring down the next pair of numbers next to the remainder. In this case, it is 44. The initial quotient is 1, so double this number (1 × 2 = 2) and write it down as the divisor’s tens place digit for the next step.
Step 4: Find the Units Place
Choose a digit for the units place of the divisor such that when the new divisor is multiplied by this digit, the product is closest to but not greater than the number you just brought down (44 in this case). Here, the correct digit is 2, making the new divisor 22 (since 22 × 2 = 44).
By following these steps, you determine that the square root of 144 by the long division method is 12. This method not only calculates square roots but also reinforces the understanding of basic multiplication and subtraction skills in a structured format.
FAQ’s
Is the Square Root of 144 a Natural Number?
Yes, the square root of 144, which is 12, is indeed a natural number. Natural numbers are whole numbers greater than zero, and since 12 fits this criteria, it is classified as a natural number.
What Square Root is Between 144?
The square root of 144 is 12. However, if we’re looking for a square root between whole numbers, we can consider that 12 is the square root of 144, and the next whole number is 13. So, there are no square roots between 12 and 13 for 144.
Is the Square Root of 144 a Perfect Square?
Yes, the square root of 144 is indeed a perfect square. A perfect square is a number that can be expressed as the product of an integer multiplied by itself. In the case of 144, it can be expressed as 12×1212×12, making it a perfect square.
Share :
