Square & Square Root of 160
Square & Square Root of 160
Square 160
The square of 160 represents the result when the number 160 is multiplied by itself.
In mathematical notation, this is expressed as 160². To determine the square of 160, you simply perform the multiplication of 160 by 160.
Mathematically, it is shown as:
160² (160 × 160) = 25,600
This calculation involves straightforward arithmetic, requiring the multiplication of 160 by itself. It is a common operation found in various mathematical fields, particularly in geometry where squaring numbers can be related to determining areas, and in algebra where exponentiation plays a key role in solving equations and exploring numeric properties.
Square Root of 160
The square root of 160 refers to the number that, when multiplied by itself, yields the product 160. In mathematical terms, finding the square root is the inverse operation of squaring. The notation for the square root of 160 is √160.
To calculate the square root of 160, you identify the number that produces 160 when squared. The calculation reveals that approximately 12.65 × 12.65 ≈ 160, indicating that 12.65 is the square root of 160.
Calculating the square root of 160 involves approximating the value since 160 is not a perfect square. However, through mathematical techniques such as estimation or using calculators, we can determine an approximate value for the square root. In this case, the square root of 160 is approximately 12.6491106407, showcasing a fundamental mathematical principle applied in various contexts, including geometry, algebra, and engineering.
Square Root of 160: 12.6491106407
Exponential Form: 160^½ or 160^0.5
Radical Form: √160
Is the Square Root of 160 Rational or Irrational?
To comprehend whether the square root of 160 is rational or irrational, let’s first define these terms.
Rational numbers are those expressible as a fraction of two integers, where the denominator is not zero, written as a/b.
Examples include 1/2, -3, and 5.
Irrational numbers, however, cannot be expressed as simple fractions of two integers. Their decimal representations are non-repeating and non-terminating.
Examples include √2, π (pi), and √3.
Square Root of 160 as Irrational:
When we calculate the square root of 160, we find that it does not simplify to a fraction of two integers. Its decimal expansion continues infinitely without repeating a pattern, indicating its irrational nature.
In summary, the square root of 160 is irrational because it cannot be expressed as a simple fraction of two integers, and its decimal expansion is non-repeating and non-terminating.
Method to Find Value of Root 160
Finding the square root of 160 involves various methods, each offering a unique approach to obtain the value. These methods are essential in mathematics and provide different strategies for calculating square roots efficiently and accurately.
- Guess and Check Method: This method involves guessing potential numbers that might be the square root of 160 and checking by squaring them. It’s straightforward and effective for perfect squares.
- Prime Factorization Method: Breaking down 160 into its prime factors (2^5 * 5) helps determine the square root by taking half the power of each prime factor.
- Long Division Method: Similar to long division, this traditional approach is useful for finding square roots, especially for non-perfect squares or when higher precision is required.
- Using a Calculator: For quick and precise results, utilizing a calculator is the simplest method. You input 160 and use the square root function to obtain the value.
Understanding and employing these methods not only facilitate the calculation of the square root of 160 but also enhance overall mathematical skills and problem-solving abilities.
Square Root of 160 by Prime Factorization Method
The prime factorization method to find the square root of 160 involves breaking down the number 160 into its basic prime factors. Prime factorization means expressing a number as the product of its prime numbers, which are numbers greater than 1 that have no divisors other than 1 and themselves.
Here’s how to use the prime factorization method for 160:
1.Divide the Number: Start by dividing 160 by the smallest prime number that can evenly divide it, which is 2. Keep dividing the quotient by 2 until you cannot evenly divide by 2 anymore.Now, 5 is a prime number, so we stop here.
- 160÷2=80
- 80÷2=4080÷2=40
- 40÷2=2040÷2=20
- 20÷2=1020÷2=10
- 10÷2=510÷2=5
2.Write Down the Prime Factors: The prime factors of 160, based on the divisions above, are 2⁵ and 5.
3.Calculate the Square Root: To find the square root, take the square root of each prime factor and multiply them. For each prime factor, divide the exponent by 2 and multiply the results.
√160 = √(2⁵× 5) = 2⁵/² × √5 =4 × √5
Therefore, the square root of 160 by the prime factorization method is 4 × √5. This method is not only useful for finding square roots but also helps in understanding the fundamental structure of numbers, enhancing one’s ability to perform various mathematical calculations.
Square Root of 160 by Long Division Method
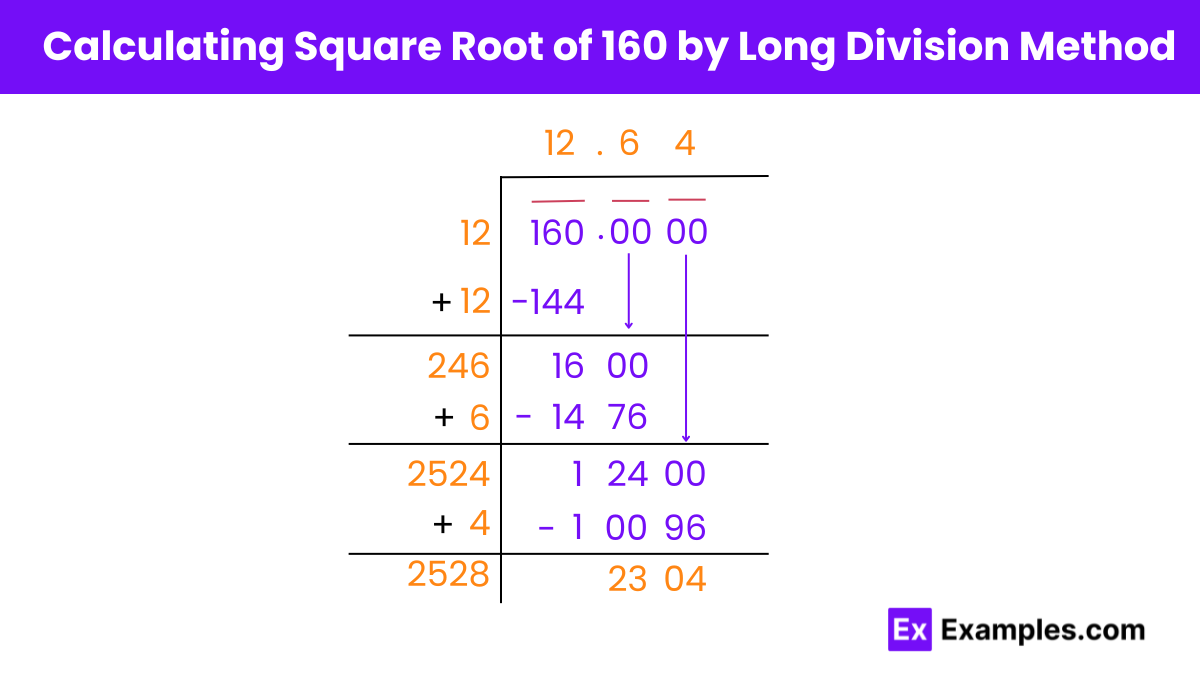
The square root of 160 by the long division method consists of the following steps:
Step 1: Starting from the right, we pair up the digits of 160 by putting a bar above 60 and 1 separately. We also pair the 0s in decimals in pairs of 2 from left to right.
Step 2: Find a number that, when multiplied to itself, gives a product less than or equal to 160. The number 12 fits here as 12 squared gives 144. Dividing 160 by 12 with the quotient as 12, we get the remainder as 16.
Step 3: Drag a pair of 0’s down and fill it next to to make the dividend 1600.
Step 4: Double the divisor 12, and enter 24 below with a blank digit on its right. Guess the largest possible digit (X) to fill in the blank and the quotient for which the product of 24X and X results in a value less than or equal to 1600. Since 6 fits the value of X, we fill 6 in the quotient after the decimal point. Divide and write the remainder.
Step 5: Repeat this process to get the desired number of decimal places.
FAQ’s
Is the square root of 160 a Natural Number?
The square root of 160 is approximately 12.65, which is not a natural number. Natural numbers are whole numbers greater than zero, without any fractions or decimals. Since 12.65 contains a decimal component, it is not considered a natural number.
What square root is between 160?
The square root of 160 is between 12 and 13. This is because the perfect square closest to 160 is 144 (12^2 = 144), and the perfect square greater than 160 is 169 (13^2 = 169). Therefore, the square root of 160 falls between 12 and 13.
Is the Square Root of 160 a Perfect Square?
No, the square root of 160 is not a perfect square. A perfect square is a number that is the square of an integer. Since 160 is not the square of any integer, its square root is not a perfect square.
Share :
