What is the square of 2?
2
4
6
8
of 10
Square & Square Root of 2 – Methods, Calculation, Formula, How to find
Square of 2
To calculate the square of 2, you simply multiply 2 by itself:
Therefore, the square of 2 is 4. This straightforward calculation is a building block for more complex mathematical operations and concepts, including algebraic equations, geometric formulas, and statistical models.
Square Root of 2
The square root of 2, denoted as √2, is a mathematical concept referring to the positive number that, when multiplied by itself, equals 2.It is an example of an irrational number, meaning it cannot be precisely represented as a fraction of two integers and has an infinite, non-repeating sequence of digits after the decimal point. The approximate value of √2 is 1.41421356237. This value is crucial in geometry, especially in calculating the diagonal of a square with sides of length 1, and it arises in various mathematical and scientific contexts due to its fundamental properties.
Exponential Form: 2^1/2 or 2^0.5
Radical Form: √2
Is the Square Root of 2 Rational or Irrational?
- A rational number is any number that can be expressed as a fraction a/b where a and b are integers, and b is not equal to zero. It includes integers, fractions, and finite or repeating decimals.
- An irrational number is a number that cannot be expressed as a simple fraction. Irrational numbers have non-repeating, non-terminating decimal expansions.
This means it cannot be expressed as a fraction of two integers (no matter how large the numbers might be), and its decimal representation goes on infinitely without repeating. The proof of the irrationality of the square root of 2 is one of the earliest known proofs in mathematics, dating back to ancient Greek mathematicians.
The essence of the proof involves assuming that √2 is rational, meaning it can be expressed as a fraction ᵃ/ᵇ, where a and b are integers with no common factors other than 1 (a fraction in simplest form). Through a series of logical steps, this assumption leads to a contradiction, showing that such a fraction cannot exist, thus proving √2 must be irrational.
Methods to Find Value of Root 2
Finding the exact value of √2 is impossible because it is an irrational number, meaning its digits go on infinitely without repeating. However, there are several methods to approximate its value with as much accuracy as needed.
Estimation Method
An estimation method involves using a simple guess-and-check approach refined over time. Here’s a basic way to estimate √2:
- Start with a guess: Know that √2 is between 1 and 2 because 1²=1 and 2²=4.
- Refine your guess: Try a number between 1 and 2, such as 1.5. Since 1.5²=2.25, which is more than 2, our next guess should be lower.
- Narrow the range: Knowing that 1.4 is a better guess (1.4²=1.96), you can keep adjusting the third decimal place. For example, you know that √2 is a bit more than 1.4 but less than 1.5.
- Continue until satisfied: Keep refining your guess within this range. For instance, trying 1.41 (1.41²=1.9881), you see it’s closer. You can continue this process, getting as close as you desire to the actual value of √2.
Square Root of 2 by Long Division Method
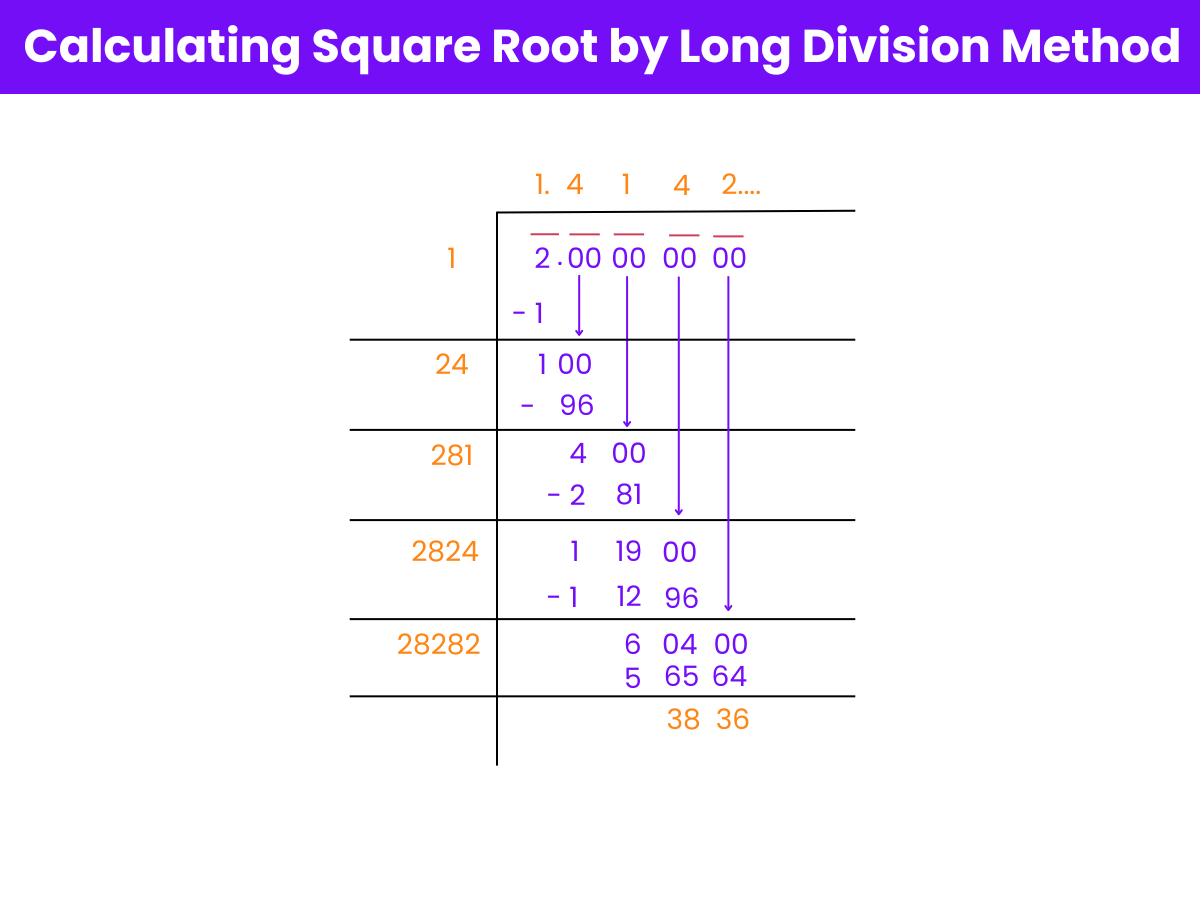
To calculate the square root of 2 using the long division method, follow these simplified steps:
Start with the closest square: Identify the largest square less than 2, which is 1 (since 1² = 1). Use 1 as both divisor and quotient, and find the remainder.
Expand the division: After getting the quotient of 1, place a decimal point and bring down two zeros, making the new dividend 100.
Double and guess: Double the divisor (making it 2) and add a blank digit to its right. Choose a digit that, when this new divisor is multiplied by it, the product is just under or equal to 100. Add this digit to the quotient and calculate the remainder.
Repeat for precision: Continue the process, doubling the new quotient part (ignoring the decimal) and adding two zeros to the remainder each time, to get more decimal places in your answer.
2 is Perfect Square root or Not
The square root of 2 is an irrational number, approximately 1.414, and cannot be expressed as the product of two identical integers. A perfect square has an integer square root.
FAQ’S
What is the square root of 2 as a number?
The square root of 2 is approximately 1.41421356237. It’s an irrational number, meaning it cannot be exactly represented as a fraction and has an infinite, non-repeating decimal expansion.
Is the square root of 2 a real number?
Yes, the square root of 2 is a real number. It’s an irrational number, meaning it cannot be expressed as a fraction, and it’s approximately equal to 1.41421356237.
Why is the square root of 2 important?
The square root of 2 is important as the first known irrational number, illustrating that not all numbers can be expressed as fractions. It’s fundamental in geometry, especially in calculating diagonals of squares.
Share :
Practice Test
Find the square root of 2.
1.41
2
1
4
of 10
What is the value of 2 raised to the power of 2?
4
8
2
6
of 10
If x² = 2, what is the value of x?
1.41
2
4
6
of 10
What is the result of 2 squared minus the square root of 2?
2.59
3
1.59
1
of 10
What is the result of the square root of 2 squared?
2
4
6
8
of 10
Calculate the product of 2 and the square root of 2.
2
4
2.828
6
of 10
What is the square root of the square of 2?
1
2
3
4
of 10
Find the number whose square is 2.
1
2
1.41
4
of 10
What is 2 raised to the power of 1/2?
1.41
2
4
0.5
of 10