Square & Square Root of 225 – Methods, Calculation, Formula, How to find

Square of 225

The square of 225 (225²) is calculated by multiplying 225 by itself:

225 × 225 = 50625.

So, the square of 225 is 50,625.

Geometrically, if you have a square with each side measuring 225 units, the total area enclosed by the square will be 50,625 square units. Understanding square number and the square of 225 is essential in various mathematical contexts, including geometry, algebra, and arithmetic. It finds applications in calculating areas, volumes, distances, and solving mathematical problems.

Square Root of 225

This is because 15 × 15 = 225.

Thus, the square root of 225 is exactly 15. This calculation is important in various mathematical and practical contexts, such as geometry, where it can represent the side length of a square with an area of 225 square units. It’s also significant in algebra and engineering, where understanding square roots helps in solving problems involving areas and other applications that require precise measurements.

Is the Square Root of 225 Rational or Irrational?

This is because 225 is a perfect square, being 15 × 15 = 225. As a result, the square root of 225 is exactly 15, which can be expressed as a fraction 15/1, making it a rational number.

Methods to Find Value of Root 225

Prime Factorization Method:

Break down 225 into its prime factors, which are 3 × 3 × 5 × 5. Pair up identical factors and take one from each pair to get 3 × 5 = 15. Therefore, the square root of 225 is 15.

Repeated Subtraction Method:

Start subtracting consecutive odd numbers from 225 until you reach 0. Count how many times you subtracted, and that count is the square root. For 225, this method will result in 15 subtractions, indicating the square root is 15.

Estimation Method:

Since 15 is a known square root close to 225, you can estimate by finding a number close to 15 that squares to 225. By trial and error, you can quickly determine that 15 is indeed the square root of 225.

Calculator:

Use a calculator with a square root function to directly find the square root of 225, which is 15.
These methods offer different approaches to find the square root of 225, catering to various preferences and situations.

Square Root of 225 by Long Division Method

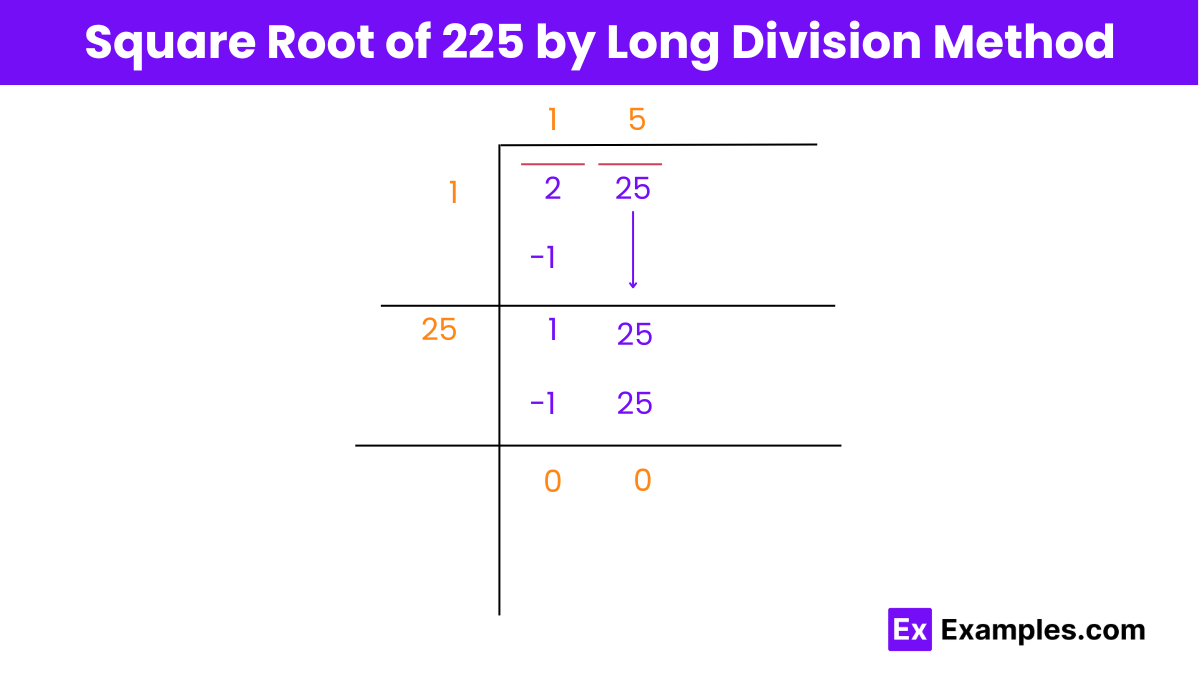
Here’s how to find the square root of 225 by the long division method:

Step 1: Start with the number 225 and group the digits into pairs from the right. So, from 225, we choose 25 as a pair, and 2 stands alone.

Step 2: We begin by dividing 2 with a number such that the number × number gives 2 or a number less than that.

Step 3: After dividing, we obtain 1 as the quotient and 1 as the remainder.

Step 4: Next, we bring down 25 for division so that the new dividend becomes 125.

Step 5: We double the divisor, meaning 1 + 1 = 2, and write this as one of the digits for the new divisor.

Step 6: Identify a number that can be placed next to 2 to obtain a two-digit number as a new divisor. This number should also be multiplied by itself to produce 125 or less than that.

Step 7: We find that 5 is the number, such that 25 × 5 gives 125.

Step 8: Finally, we obtain the quotient 15 and the remainder as 0.

By following these steps, we have successfully found that the square root of 225 is 15 using the long division method.

225 is Perfect Square Root or Not

A perfect square is a number that can be expressed as the product of an integer multiplied by itself. In the case of 225, it can be expressed as 15 × 15, which equals 225. Therefore, 225 is indeed a perfect square.

FAQ’s

What are the basic factors of 225?

The basic factors of 225 are 1, 3, 5, 15, and 225. These numbers can be multiplied together to get 225, making them its basic factors.

Is 225 a perfect cube?

No, 225 is not a perfect cube.

A perfect cube is a number that can be expressed as the product of an integer multiplied by itself twice.