Square & Square Root of 24
Square of 24
To calculate the square of 24, you multiply 24 by itself:
Therefore, the square Numbers of 24 is 576. This calculation involves multiplying 24 by itself, resulting in 576. This concept is fundamental in various mathematical operations, serving as a basis for algebraic equations, geometric formulas, and statistical models.
Square Root of 24
The square root of 24 is an irrational number, similar to the square root of 21, as it cannot be precisely expressed as a fraction of two integers. Its approximate value is 4.89897948557. This value is significant in various mathematical applications, including geometry, where it represents the length of the side of a square with an area of 24 square units. Additionally, the square root of 24 appears in algebraic equations, engineering calculations, and physics formulas, contributing to the understanding of spatial relationships and numerical approximations.
Approximate Decimal Form: 4.89897948557
Exponential Form: 24^0.5 or 24¹/²
Radical Form: √24
Is the Square Root of 24 Rational or Irrational?
The square root of 24 is an irrational number, meaning it cannot be expressed as a simple fraction of two integers. Its decimal representation is non-terminating and non-repeating, indicating its irrational nature. The approximate value of √24 is 4.89897948557.
This value holds significance in various mathematical contexts, including geometry, where it represents the length of the side of a square with an area of 24 square units. Additionally, the square root of 24 appears in algebraic equations, engineering calculations, and physics formulas, contributing to the understanding of spatial relationships and numerical approximations.
Methods to Find Value of Root 24
There are several methods to find the value of the square root of 24. Here are some common approaches:
-
Estimation Method:
- Approximate the square root of 24 by comparing it to the square roots of nearby perfect squares.
- Since 16 < 24 < 25, we know that √16 < √24 < √25.
- Therefore, 4 < √24 < 5.
- This gives us a rough estimate that the square root of 24 lies between 4 and 5.
-
Prime Factorization Method:
- Express 24 as a product of prime factors: 24 = 2 × 2 × 2 × 3.
- Take out pairs of similar numbers: √24 = √(2 × 2 × 2 × 3) = 2√6.
- Find the square root of the remaining factor, if possible.
- √6 is left, and it cannot be further simplified because 6 is not a perfect square.
-
Calculator or Computer Software:
- Use a scientific calculator or computer software to compute the square root of 24 directly.
- This method provides an accurate decimal approximation of √24, such as 4.89897948557.
Square Root of 24 by Long Division Method
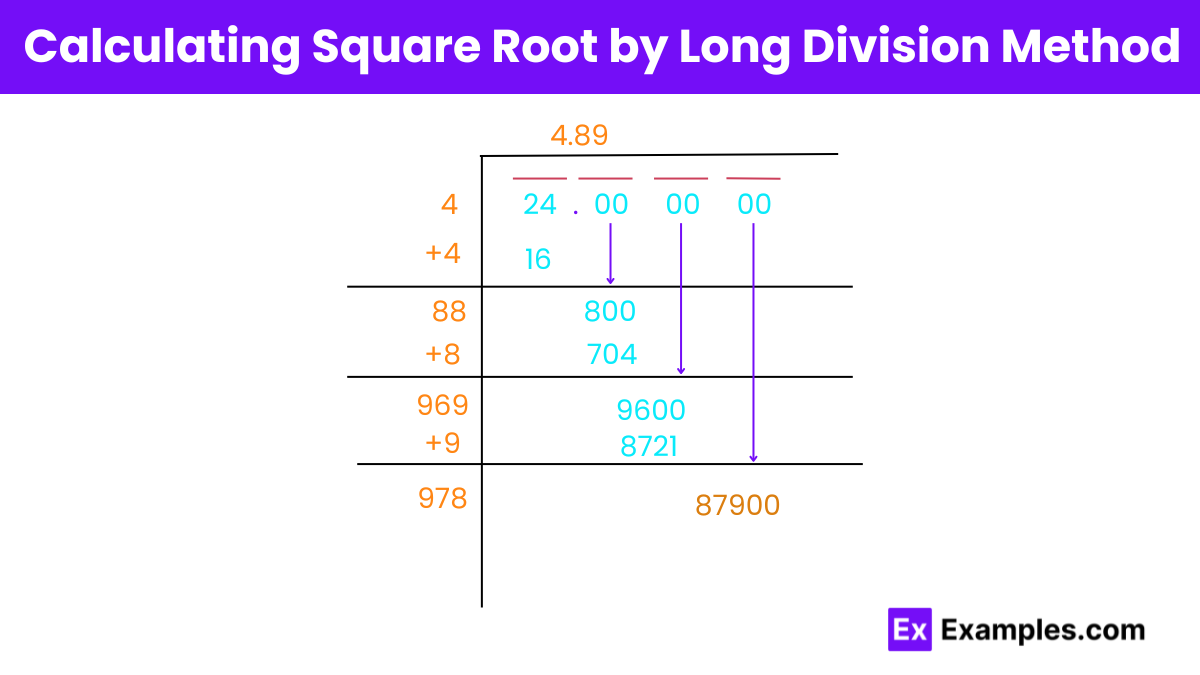
Step 1: Set Up the Number Place the number 24 under a square root sign. Since 24 is not a perfect square, extend it with decimal places (as pairs of zeros) for the desired precision. For instance, to find the square root of 24 up to four decimal places, write it as 24.0000 0000, grouped as 24.00 00 00 00.
Step 2: Find the Largest Square Identify the largest square smaller than or equal to the first pair. For 24, the largest perfect square less than or equal to 24 is 16 (4²). Write 4 above the square root sign as the first digit of the result.
Step 3: Subtract and Bring Down the Next Pair Subtract the square of your result (4) from the first pair (24) and bring down the next pair of digits (00), making it 100.
Step 4: Double the Divisor Double the number you’ve already found (4) to get 8. This is the new divisor.
Step 5: Find the Next Digit Find a digit (D) that, when you append it to the divisor and multiply the new number by D, gets as close as possible to your current number (100) without exceeding it. This step involves estimation and checking.
Step 6: Repeat the Process Subtract the result of your multiplication from the current number. Bring down the next pair of zeros. Double the current result (not including the new digit) and find the next digit so that when this doubled number with the new digit at the end is multiplied by the new digit, it is as close as possible to the new current number without going over.
Step 7: Continue Until Satisfied Keep repeating the process, adding pairs of zeros and calculating subsequent digits of the square root. You can continue this for as many decimal places as you require.
24 is Perfect Square root or Not?
A perfect square is a number that can be expressed as the product of an integer multiplied by itself. For example, 4, 9, and 16 are perfect squares because they can be written as 2², 3², and 4² respectively. However, 24 cannot be expressed as the square of an integer, so it is not a perfect square.
FAQ’s
What is the simplified form of √24?
In Maths, the square root of 24 is equal to 2√6 in radical form and 4.898979485 in decimal form. The product of the square root of a number with itself produces the original number.
What does the square root of 24 lie between?
As 24 lies between 16 and 25, the square root of 24 must be greater than the square root of 16 and less than the square root of 25. This means the square root of 24 lies between the integers four and five. 24 is closer to 25 than 16.
What is the greatest perfect square of 24?
We should try to reduce √24 to the root of a number with a perfect square multiplied by some other whole number. Out of these, 4 is the largest (and coincidentally, only) perfect square present.
Share :
