Square & Square Root of 25

Square of 25

25² (25×25) =625

The square of 25, denoted as 25×25, equals 625. In mathematics, squaring a number means multiplying it by itself. So, to find the square of 25, you multiply 25 by 25. This results in 625, which is the product of 25 multiplied by itself. Visually, you can represent this as a square with sides of length 25 units, where the area of the square is 625 square units. Understanding squares and their values is fundamental in various mathematical concepts and applications, ranging from geometry to algebraic equations.

Square Root of 25

√25 = 5

The square root of 25, denoted as √25, is equal to 5. In mathematics, the square root of a number is a value that, when multiplied by itself, gives the original number. So, for 25, the square root is 5 because 5 multiplied by itself equals 25. This can also be represented as √25 = 5. Understanding square roots is essential in various mathematical calculations, such as finding the side length of a square with a given area or solving quadratic equations. In real-world scenarios, square roots are commonly used in fields like engineering, physics, and finance.

Square Root of 25: 5

Exponential Form of 25: (25)^½ or  or (25)^0.5 

Radical Form of 25: √25

Is the Square Root of 25 Rational or Irrational?

Square Root of 25 is a Rational Number.

Rational: The square root of 25 is rational. A rational number is one that can be expressed as a fraction of two integers. In the case of the square root of 25, it equals 5, which can be represented as the fraction 5/1. This indicates that 5 is a rational number because it can be expressed as a ratio of two integers.

Irrational: None. Since the square root of 25 is rational, it does not have any irrational component. Irrational numbers cannot be expressed as fractions of integers, but the square root of 25 can be represented as the rational number 5. Therefore, it does not possess any irrational characteristics.

Methods to Find Value of Root 25

Finding the square root of a number involves determining the value that, when multiplied by itself, gives the original number. For example, the square root of 25 is the value that, when multiplied by itself, equals 25. There are various methods to find the square root of a number, ranging from simple arithmetic techniques to more complex mathematical algorithms.

1. Prime Factorization: Express 25 as a product of prime numbers (5 × 5), then take one factor of 5, giving you the square root of 25 as 5.
2. Repeated Subtraction: Start with a number close to the square root of 25 (e.g., 4). Subtract it from 25 and adjust the number based on the result until you get 0. This iterative process yields the square root, which is 5.
3. Guess and Check: Estimate the square root of 25 (e.g., 4 or 6) and square it. Adjust your guess based on whether the result is too high or too low until you find the correct value, which is 5.
4. Using a Calculator: Simply input √25 into a calculator, and it will give you the result directly, which is 5.
5. Geometric Method: Draw a square with an area of 25 square units. Then, find the side length of the square, which is the square root of 25, giving you a value of 5 units.
6. Binomial Theorem: Expand (a + b)^2 = 25, where a = b. Solving this equation yields a value of a = 5, which is the square root of 25.
7. Using Tables: Refer to precomputed tables of square roots to find the value corresponding to 25, which is 5.

Square Root of 25 by Long Division Method

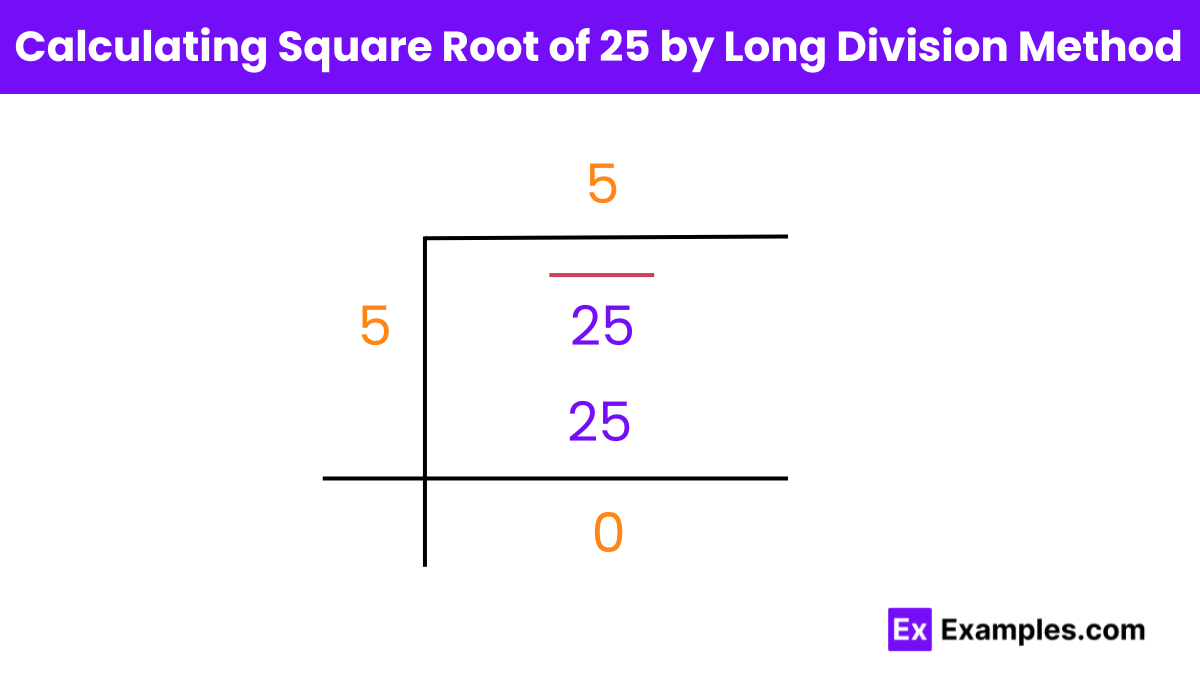
To find the square root of 25 using the long division method, you essentially break down the number into pairs of digits from right to left (in this case, just 25 since it’s a two-digit number) and then find a number which, when multiplied by itself, gives a product less than or equal to 25. The steps are as follows:

1. Set Up: Write down 25 and draw a long division bar over it. Since 25 is a two-digit number, it’s already in a single pair.
2. Division: Start with the first digit. Find a number that, when squared, is less than or equal to 25. In this case, 5 × 5 = 25.
3. Subtraction: Subtract 25 (the result of 5 × 5) from 25, which leaves you with 0.
4. Bring Down Pairs: Normally, if there were more digits, you’d bring down the next pair of digits next to the remainder. However, since there are no more digits in 25, the process ends here.
5. Find the Next Digit: If we were continuing (such as with larger numbers), we’d double the current quotient (which is 5), and find the next digit of the square root by guessing and checking a digit (X) that fits in the expression (10×5 + X)×X ≤ remainder, adjusting until finding the correct digit.

For 25, the process concludes quickly as 5 squared exactly equals 25, leaving no remainder. Therefore, the square root of 25 by the long division method is determined to be 5, with no further digits to calculate. This method is particularly useful for larger numbers or for finding more precise square roots that might not be whole numbers.

FAQS

Is √25 a perfect square?

Yes, √25 is a perfect square because 25 is the product of 5 multiplied by itself (5 × 5). A perfect square results from a whole number multiplied by itself.

Is the square root of 25 a whole number?

Yes, the square root of 25 is a whole number. The square root of 25 is 5, which is a whole and integer value, indicating that 25 has an exact square root.

What is the perfect square of 25?

The perfect square of 25 is 625. This is because when you multiply 25 by itself (25 × 25), the result is 625, which makes it the perfect square of 25.

How is the square root of 25 equal to 5?

The square root of 25 is 5 because when you multiply 5 by itself (5 × 5), the result is 25. The square root operation essentially asks what number, when squared, equals 25, and in this case, it’s 5.

How many digits are there in the square root of 25?

There is 1 digit in the square root of 25. The square root of 25 is 5, which is a single-digit number, illustrating the simplicity of the square root in this instance.

In conclusion, the square of 25 is 625, resulting from multiplying 25 by itself. The square root of 25, on the other hand, is 5, as 5 multiplied by 5 gives 25. These operations demonstrate the fundamental concepts of squaring and square rooting in mathematics, providing a clear example of how numbers interact within these processes to produce whole number results.