Square & Square Root of 250
Square of 250
To calculate the square of 250, you multiply 250 by itself:
Thus, the square of 250 is 62500. This process involves taking 250 and multiplying it by 250 once again, yielding a product of 62500. Squaring a number is a fundamental mathematical operation with wide applications across different fields such as algebra, statistics, engineering, and economics.
Square Root of 250
The square root of 250 is an irrational number, and it is approximately 15.81 when rounded to two decimal places. This value is derived because 15.81 multiplied by itself (15.81 × 15.81) approximates 250. The square root function determines what number, when multiplied by itself, produces the original number—in this case, 250.
Understanding the square root is essential in various fields of mathematics and its applications, such as calculating the diagonal of a rectangle, simplifying algebraic expressions, or in physics and engineering, where it plays a role in formulas and models.
Square Root of 250: 15.81
Exponential Form: 250^½ or 250^0.5
Radical Form: √250
Is the Square Root of 250 Rational or Irrational?
Here’s a simple way to understand this: A rational number is any number that you can write as a fraction where both the numerator (top number) and the denominator (bottom number) are whole numbers. An irrational number, on the other hand, cannot be written this way because it has a decimal that goes on forever without repeating.
For the square root of a number to be rational, that number must be a perfect square (like 4, 9, 16, etc., where the square roots are 2, 3, 4, respectively). Since 250 is not a perfect square—meaning no whole number multiplied by itself gives exactly 250—its square root does not result in a whole number or a simple fraction. Therefore, the square root of 250, which is about 15.81, is an irrational number with a decimal that never ends or repeats.
Methods to Find Value of Root 250
To find the square root of 250 in a way that’s easy to understand, here are three methods you can use:
1.Using a Calculator: This is the simplest method. Just type 250 into a calculator and press the square root button (√). The calculator will show you that the square root of 250 is approximately 15.81. This method is fast and doesn’t require any math skills beyond being able to use a calculator.
2.Simplification Method: Start by breaking down the number 250 to make it easier to work with. You know that 250 can be split into 25 and 10.
Since 25 is a perfect square (because 5×5 = 25), you can take the square root of 25 easily, which is 5.
Now, you’re left with finding the square root of 10, which you can’t do exactly without a calculator, but you know it’s a little more than 3 because 3 × 3 = 9.
Multiply 5 (the square root of 25) by a bit more than 3 (an estimate of the square root of 10), and you get a little more than 15, which is close to the actual square root of 250.
3.Estimation by Comparing Perfect Squares: Look for perfect squares close to 250 to guess its square root. The perfect squares nearest to 250 are 225 (15 squared) and 256 (16 squared).
Since 250 is closer to 225 than 256, you can guess that the square root of 250 is closer to 15.
To be more precise, 250 is 25 units above 225 and 6 units below 256. It’s much closer to 225, so you can guess that the square root of 250 is a bit more than 15, perhaps around 15.5 or a little higher.
These methods range from very precise to general estimates, depending on whether you have a calculator or if you’re trying to understand the concept with simple math.
Square Root of 250 by Long Division Method
Step-by-Step Process of Long Division Method to Find √250
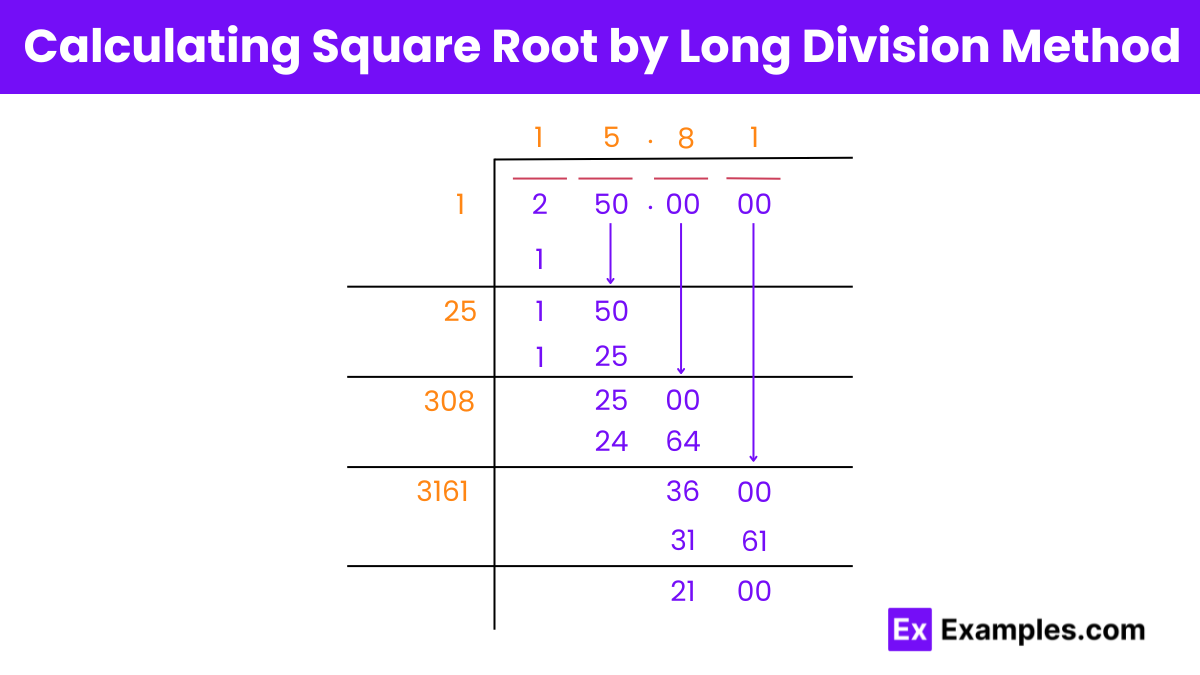
Step 1: Pair the digits of the number from the right.
- Pair digits from the one’s place. For 250, we have two pairs: [2], [50]. Since there is only one digit in the first pair, we will begin our process with [2].
Step 2: Find the first digit of the square root
Find the largest number whose square is less than or equal to the first pair or first number. When we square 1, the result is 1, which is less than 2. We then subtract this square (1) from the initial pair (2), and bring down the next pair of digits to continue the division process.
Step 3: Double the quotient and determine the next digit.
- Double the quotient (now 1) to get 2. We need to find a digit X such that when placed next to 2 (forming 2X), the product of 2X and X is less than or equal to 150. The digit 5 works (25 × 5 = 125). Subtract 125 from 150 to get a remainder of 25.
Step 4: Extend the process with a decimal.
- Now, double the current quotient (15) to get 30. Add a decimal point to the quotient and bring down a pair of zeros to the remainder, making it 2500.
- Find a digit X such that when added to 30 (forming 30X), the product of 30X and X is less than or equal to 2500. The digit 8 works (308 × 8 = 2464). Subtract 2464 from 2500 to get a remainder of 36.
Step 5: Continue extending the process.
- Double the current quotient (158) to get 316. Bring down another pair of zeros to the remainder, making it 3600.
- Find a digit X such that when added to 316 (forming 316X), the product of 316X and X is less than or equal to 3600. The digit 1 works (3161 × 1 = 3161). Subtract 3161 from 3600 to get a remainder of 439.
Step 6: Repeat as necessary.
- Continue this process, doubling the whole quotient and bringing down more zeros, to find each subsequent digit of the square root as needed for the desired accuracy.
Your outline captures the essence of the long division method well, but it helps to provide clear step-by-step operations, especially explaining how digits are chosen and how the quotient and remainder are updated, which is crucial for understanding and applying the method accurately.
250 is Perfect Square root or Not?
A perfect square is a number that’s the product of an integer multiplied by itself. For example, 16 is a perfect square because it equals 4 times 4.
For 250, there’s no whole number that you can multiply by itself to get exactly 250. The square of 15 is 225, and the square of 16 is 256. Since 250 doesn’t fit this pattern (it’s not 15^2 and not 16^2), it is not a perfect square.
FAQ’S
What is the simplest form of √ 250?
The simplest form of √250 is 5√2. This is found by factoring 250 into 2×5² and taking the square root of each factor.
What is the square root of 250 to the nearest whole number?
The square root of 250 to the nearest whole number is 16. This is calculated by finding the exact square root (approximately 15.81) and rounding it to the nearest whole number.
Share :
