Square & Square Root of 2500
Square of 2500
To calculate the square of 2500, you multiply 2500 by itself:
Therefore, the square Numbers of 2500 is 6,250,000. This calculation is achieved by multiplying 2500 by itself, resulting in 6,250,000. Understanding how to find the square of a number is crucial in various mathematical fields including algebra, geometry, and data analysis, as it provides a foundation for tackling more intricate problems and concepts.
Square Root of 2500
This is because 50 × 50 = 2500.
Thus, the square roots of 2500 is exactly 50. This calculation is important in various mathematical and practical contexts, such as geometry, where it can represent the side length of a square with an area of 2500 square units. It’s also significant in algebra and engineering, where understanding square roots helps in solving problems involving areas and other applications that require precise measurements.
Square Root of 2500 : 50
Exponential Form : 2500^½ or 2500^0.5
Radical Form : √2500
Is the Square Root of 2500 Rational or Irrational?
The square root of 2500 is rational because it equals 50, a whole number. Rational numbers include all integers, fractions, and decimals that can end or repeat. Since 50 is a clear, whole number, it’s definitely rational.
Method to Find Value of Root 2500
To find the square root of 2500, you can use a couple of different methods, depending on the tools available and the level of accuracy you require. Here are two common methods:
Estimation and Rounding
This method involves estimating and refining your guess based on known squares:
You Know that 50² = 2500.This method quickly confirms the square root since 2500 is a perfect square.
Using a Calculator
For precise computation, especially when dealing with non-perfect squares, a calculator is the simplest and most accurate method:
Simply enter 2500 and then press the square root function
Prime Factorization
This method is useful especially for educational purposes to understand the structure of a number:
Factorize 2500 into its prime factors: 2500 = 2² × 5⁴.
Each of these methods can help determine the square root of 2500, with some providing more insight into the mathematical structure than others.
Square Root of 2500 by Long Division Method
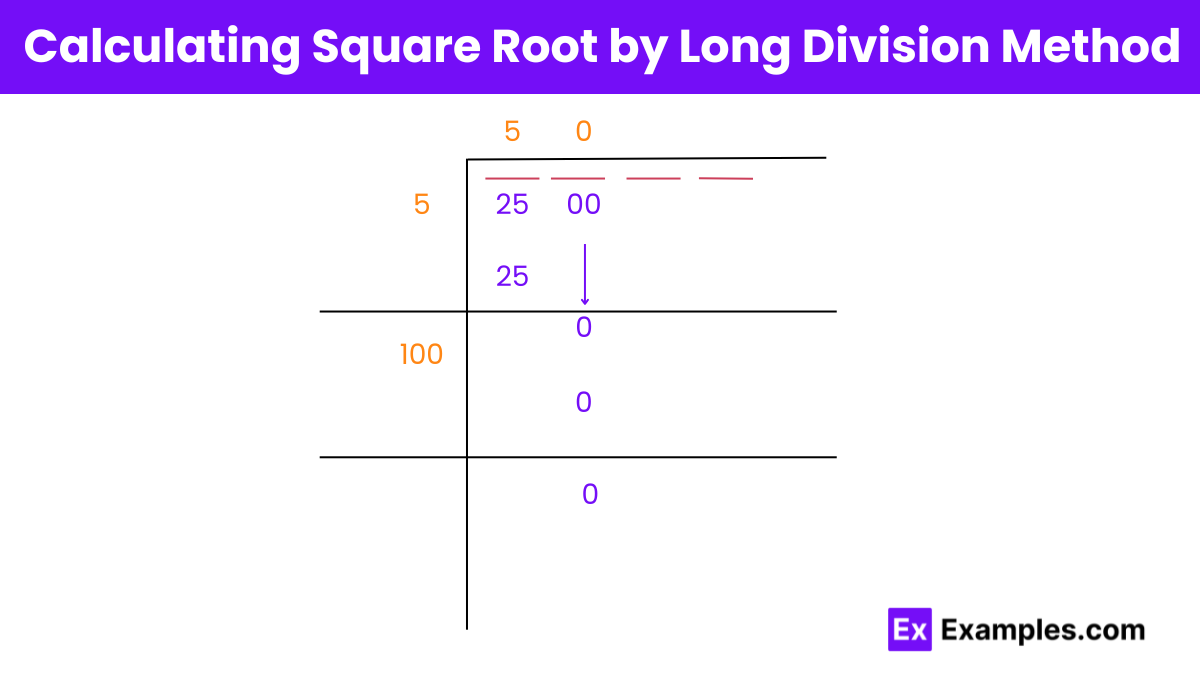
Step 1: Arrange the Number
Group the digits into pairs from right to left: For 2500, you have the pairs 25 and 00.
Step 2: Find the First Digit of the Root
Identify the largest number whose square is less than or equal to 25. The largest number is 5 because 5²=25.
Write down 5 as part of your answer because 5 is the square root of 25.
Step 3: Subtract and Bring Down
Subtract 25 from 25 to get 0. Bring down the next pair of zeros, making it 000.
Step 4: Double the Quotient and Find the Next Digit
Double the quotient (5 becomes 10).
Attach a 0 next to 10 making it 100 since 100 × 0=0 which fits into 000.
Step 5: Complete the Process
There are no more digits to bring down, so the process ends here.
Your final answer is 50 because the calculation fits perfectly without remainder.
2500 is Perfect Square root or Not?
A perfect square is a number that can be expressed as the square of an integer. In the case of 2500, it is the square of 50:
50 × 50 = 2500
Since 50 is an integer, and multiplying it by itself results in 2500, this confirms that 2500 is indeed a perfect square.
FAQ’s
What are the multiples of 2500?
The first 10 multiples of 2500 are 2500, 5000, 7500, 10000, 12500, 15000, 17500, 20000, 22500 and 25000.
Share :
