Square & Square Root of 26
Square of 26
The square of 26 is calculated by multiplying 26 by itself. When you do this, 26 × 26, the result is 676. This process of squaring signifies taking a number and raising it to the power of 2, which in mathematical terms is expressed as 262262. The outcome, 676, is a reflection of the exponential increase that occurs when a number is squared, showcasing a fundamental concept in algebra that has applications in various areas such as geometry, where it can represent the area of a square with each side measuring 26 units.
Square Root of 26
Or
√26 = 5.099 up to three places of decimal.
The square root of 26 is the number that, when multiplied by itself, equals 26. Unlike perfect squares like 16 or 25, 26 is not a perfect square, so its square root does not result in a whole number. The square root of 26 is approximately 5.099, a decimal number that extends indefinitely without repeating, which is a characteristic of irrational numbers. In mathematical notation, this is represented as √26 ≈ 5.099. This concept is crucial in various mathematical applications, including geometry and algebra, where understanding the properties of square roots can help solve equations and analyze shapes.
Exponential Form of 26: (26)½ or or (26)0.5
Radical Form of 26: √26
Is the Square Root of 26 Rational or Irrational?
The Square Root of 26 Irrational Number
Rational
Rational numbers are those that can be expressed as a fraction or quotient of two integers, where the denominator is not zero. For a number to be rational, its decimal representation must either terminate after a finite number of digits or repeat a sequence of digits infinitely.
Irrational
The square root of 26 is irrational. This means it cannot be precisely expressed as a fraction of two integers. Its decimal form is non-terminating and does not repeat a specific pattern of digits. The square root of 26, when calculated, gives a decimal that continues indefinitely, making it an irrational number. This is characteristic of most square roots of non-perfect squares.
Methods to Find Value of Root 26
Finding the square root of a number involves determining the value that, when multiplied by itself, gives the original number. For example, the square root of 26 is the value that, when multiplied by itself, equals 26. There are various methods to find the square root of a number, ranging from simple arithmetic techniques to more complex mathematical algorithms.
- Prime Factorization: Express 26 as a product of prime numbers and extract the square root from the prime factors.
- Repeated Subtraction: Start with a number close to the square root of 26 and subtract it iteratively from 26 until reaching 0.
- Guess and Check: Estimate the square root of 26 and square it to see if the result is close to 26. Adjust your guess until you find the correct value.
- Using a Calculator: Simply input √26 into a calculator to obtain the square root directly.
- Newton’s Method: Use Newton’s method of successive approximations to iteratively improve an initial guess of the square root of 26.
- Approximation Methods: Utilize approximation techniques such as the Babylonian method to approximate the square root of 26.
- Geometric Method: Construct a square with an area of 26 square units and find the length of its side to determine the square root of 26.
- Table Lookup: Refer to precomputed tables of square roots to find an approximation of the square root of 26.
Square Root of 26 by Long Division Method
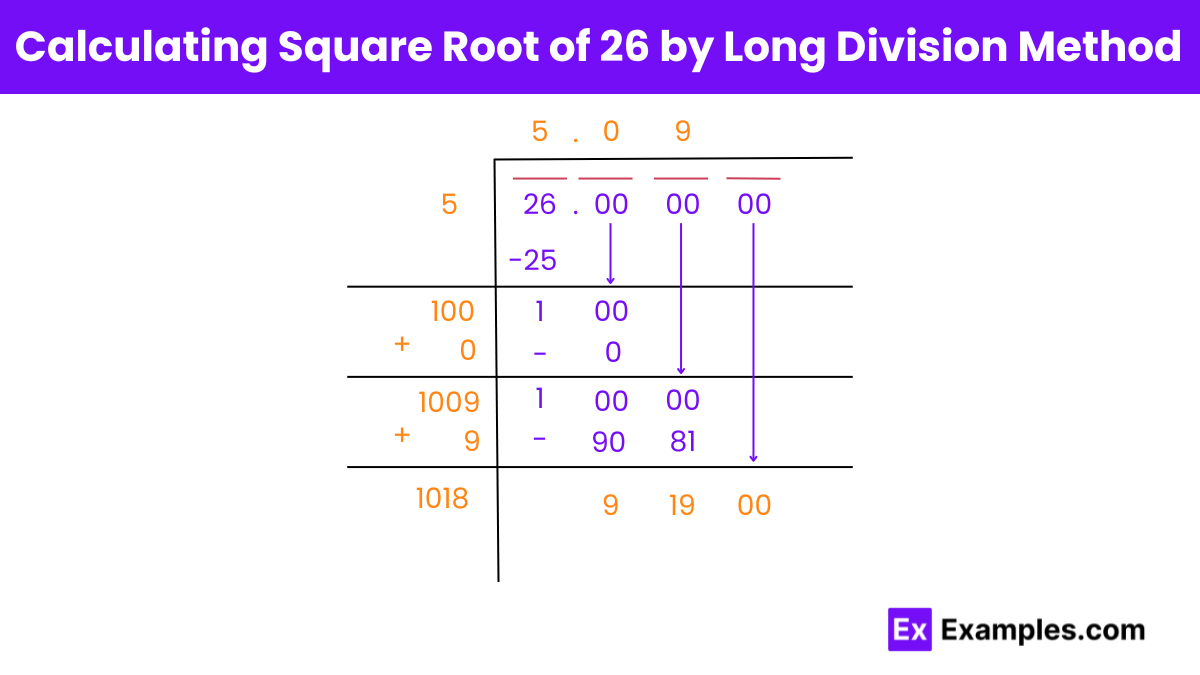
The long division method is a technique used to find the square root of a number by repeatedly subtracting perfect squares. Here’s how it’s applied to find the square root of 26:
- Group the digits of 26 into pairs from the decimal point: (26).
- Start with the largest digit that, when squared, is less than or equal to 26, which is 5 (since 5^2 = 25).
- Subtract 25 from 26, leaving 1.
- Bring down the next pair of zeros to the right of 1, making it 100.
- Double the quotient (5) to get 10 and write it as the divisor with a blank space for a placeholder.
- Find the largest digit that, when added to the divisor (10), produces a number less than or equal to 100, which is 0.
- Write down 0 next to the divisor and subtract (10 + 0)^2 = 100 from 100, leaving no remainder.
- Since there are no more digits to bring down, the process stops here.
So, the square root of 26, rounded to three decimal places, is approximately 5.099.
FAQS
Why is 26 not a perfect square?
26 is not a perfect square because there is no whole number that, when multiplied by itself, equals 26. Perfect squares are the product of an integer multiplied by itself, like 25 (5×5) or 36 (6×6). Since no whole number squared equals 26, it cannot be a perfect square.
What is the simplest form of 26?
The simplest form of 26 is just 26 itself, as it is a whole number that cannot be simplified further. In terms of prime factorization, 26 can be broken down into 2×13, but as a single whole number, it is already in its simplest form.
How do you simplify √26?
Since 26 is not a perfect square, √26 cannot be simplified into a whole number. Its simplest form remains as √26. However, you can estimate √26 using decimal or fractional approximations, or express it in terms of the square roots of its prime factors: √(2×13).
What is 26 divided by 3 simplified?
When 26 is divided by 3, the quotient is approximately 8.6667. Simplifying this as a fraction gives 8 2/3. Since 26 is not evenly divisible by 3, you are left with a fractional or decimal remainder, with 8 2/3 being the simplified fraction form.
What two numbers equal 26?
Any two numbers that add up to 26 can equal 26, such as 13 + 13, 20 + 6, or 25 + 1. There are infinite pairs of numbers, including whole numbers, fractions, and decimals, that can sum up to 26 when added together.
In conclusion, the square of 26, achieved by multiplying 26 by itself, results in 676, demonstrating the exponential increase characteristic of squaring numbers. Conversely, the square root of 26, which identifies a number that when squared gives 26, does not yield a whole number due to 26 not being a perfect square, leading to an irrational square root approximately equal to 5.099.
Share :
