Square & Square Root of 27 – Methods, Calculation, Formula, How to find

Square of 27

The square of 27, denoted as 27^2, equals 729. To compute it, you multiply 27 by itself, resulting in 729. In mathematical terms, squaring a number means raising it to the power of 2. Visually, you can represent the square of 27 as a square with sides of length 27 units, where the area of the square is 729 square units. Understanding squares and their values is fundamental in various mathematical concepts and applications, such as geometry, algebra, and calculating areas or volumes. In real-world scenarios, knowing the square of 27 aids in calculations involving quantities or measurements squared.

Square Root of 27

The square root of 27, denoted as √27, is approximately 5.196. To find it, we seek a number that, when multiplied by itself, equals 27. Since 5^2 equals 25 and 6^2 equals 36, we estimate the square root to be between 5 and 6. Using methods like approximation or algorithms such as Newton’s method, we refine the estimate to approximately 5.196. The square root of 27 is an irrational number, meaning its decimal representation is non-repeating and non-terminating. Understanding square roots aids in various mathematical calculations, including geometry, physics, and engineering.

Is the Square Root of 27 Rational or Irrational?

The Square Root of 27 Irrational Number.

In mathematics, numbers are categorized into rational and irrational based on their properties. Rational numbers can be expressed as fractions of integers, while irrational numbers cannot and have non-repeating, non-terminating decimal expansions.

Rational: The square root of 27 is irrational. A rational number can be expressed as a fraction of two integers, but the square root of 27 cannot be simplified into such a form. This is because 27 does not have a perfect square root that results in a whole number. Therefore, the square root of 27 is an irrational number.

Irrational: The square root of 27 is irrational. Irrational numbers cannot be expressed as fractions of integers, and they have non-repeating, non-terminating decimal expansions. Since the square root of 27 does not result in a whole number and cannot be expressed as a fraction, it falls into the category of irrational numbers.

Methods to Find Value of Root 27

Finding the square root of a number involves determining a value that, when multiplied by itself, results in the original number. In the case of 27, its square root is a value that, when squared, equals 27. There are various methods to find the square root of 27, each with its own approach and level of complexity.

1. Prime Factorization: Express 27 as a product of prime numbers and extract the square root from the prime factors.
2. Repeated Subtraction: Start with a guess (e.g., 5) and subtract it from 27, adjusting the guess until the difference approaches zero.
3. Guess and Check: Estimate the square root of 27 and square it, adjusting the guess until you reach the closest approximation.
4. Using a Calculator: Simply input √27 into a calculator to obtain the square root directly.
5. Newton’s Method: Apply Newton’s method of successive approximations to refine an initial guess of the square root of 27.
6. Approximation Methods: Utilize approximation techniques such as the Babylonian method to approximate the square root of 27.
7. Geometric Method: Construct a square with an area of 27 square units and find the length of its side to determine the square root.
8. Table Lookup: Refer to precomputed tables of square roots to find an approximation of the square root of 27.

Square Root of 27 by Long Division Method

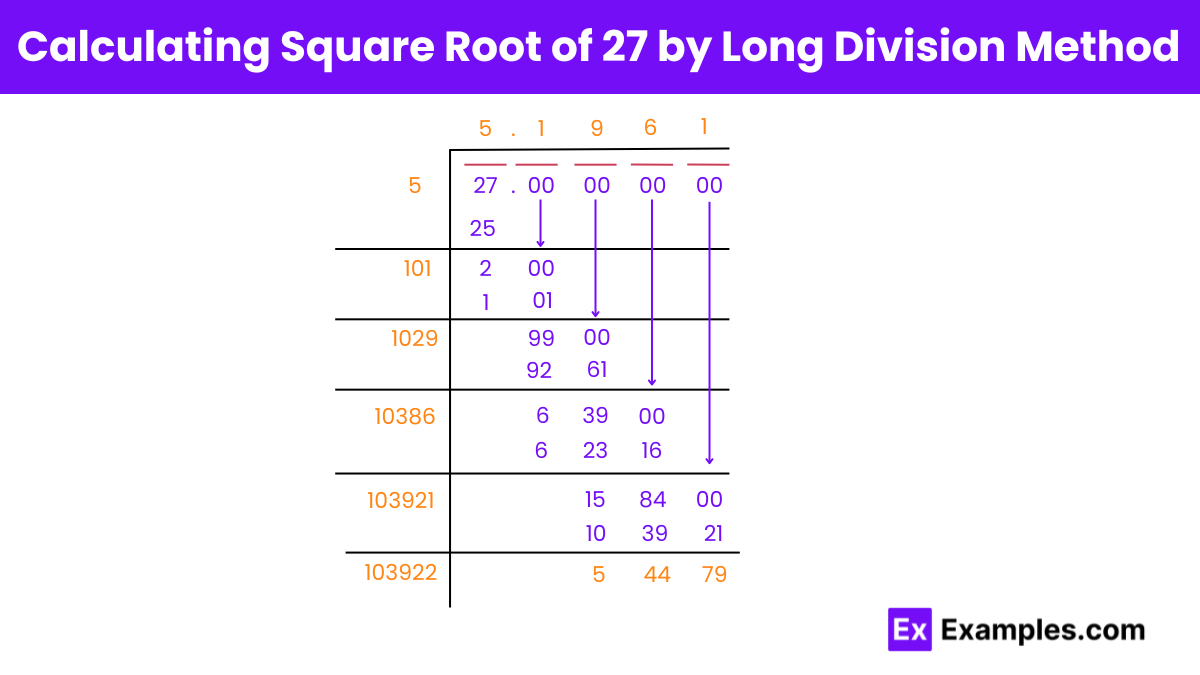
The long division method is a technique used to find the square root of a number by repeatedly subtracting perfect squares. In the case of finding the square root of 27, this method involves a step-by-step process of division and subtraction to approximate the square root.

Steps to Find the Square Root of 27 by Long Division:

1. Group Digits: Group the digits of 27 into pairs from the decimal point (27).
2. Starting Digit: Start with the largest digit that, when squared, is less than or equal to 27. In this case, it’s 5 (since 5^2 = 25).
3. Subtraction: Subtract 25 from 27, leaving 2.
4. Bring Down: Bring down the next pair of zeros to the right of 2, making it 200.
5. Divisor: Double the quotient (5) to get 10 and write it as the divisor with a blank space for a placeholder.
6. Next Digit: Find the largest digit that, when added to the divisor (10), produces a number less than or equal to 200. The digit is 4 (since (10+4)^2 = 196).
7. Subtraction: Write down 4 next to the divisor and subtract (10 + 4)^2 = 196 from 200, leaving a remainder of 4.
8. No More Digits: Since there are no more digits to bring down, the process stops here.

By following these steps, the square root of 27, rounded to three decimal places, is approximately 5.196.

FAQS

What is the perfect square for 27?

There is no perfect square for 27, as 27 itself is not a perfect square. A perfect square is a number that is the square of an integer. The nearest perfect squares to 27 are 25 (5²) and 36 (6²).

Why is the square root of 27 irrational?

The square root of 27 is irrational because it cannot be expressed as a fraction of two integers. Its decimal representation is non-repeating and non-terminating. Since 27 is not a perfect square, its square root does not result in a whole number, making it irrational.

Is √27 natural?

√27 is not considered a natural number. Natural numbers are the set of positive integers starting from 1. Since the square root of 27 is an irrational number and not a whole number, it does not fit into the category of natural numbers.

Why 27 is not a prime number?

27 is not a prime number because it has more divisors than just 1 and itself. It can be divided evenly by 1, 3, 9, and 27. For a number to be considered prime, it must only be divisible by 1 and itself, which is not the case with 27.

Can √27 be simplified?

√27 can be simplified to 3√3. This simplification comes from the fact that 27 is equal to 9 * 3, where 9 is a perfect square. By taking the square root of 9, which is 3, and placing it outside the radical, √27 becomes 3√3, which is its simplest radical form.

In conclusion, the square of 27 is 729, a straightforward calculation where 27 is multiplied by itself. On the other hand, the square root of 27, approximately 5.196, is an irrational number because it cannot be precisely expressed as a fraction. The nature of 27 as neither a perfect square nor a prime number adds to the complexity of its square and square root properties.