Square & Square Root of 32
Square of 32
To calculate the square of 8, you simply multiply32 by itself:
Therefore, the square of 32 is 1024.Geometrically, if you have a square with each side measuring 32 units, the total area enclosed by the square will be 1024 square units.
Understanding the square of 32 is essential in various mathematical contexts, including geometry, algebra, and arithmetic. It is a fundamental operation that finds applications in numerous real-world scenarios, such as calculating areas, volumes, distances, and solving mathematical problems.
Square Root of 32
Or
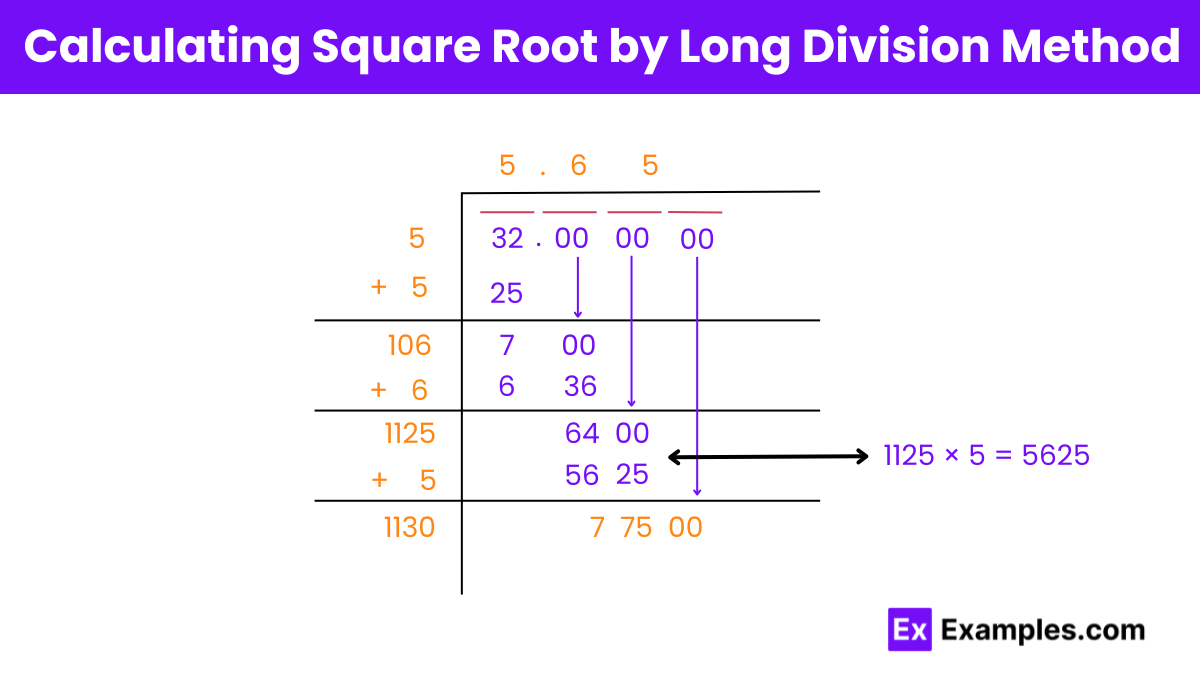
√32 = 5.656 up to three places of decimal
Mathematically, √32 represents the non-negative number whose square is equal to 32. In other words:
√32×√32 = 32
The square root of 32 can be expressed in radical form as √(2×16), where 16 is a perfect square. This simplifies to 4√2.
So, √32 = 4√2, where 4 is the numerical coefficient and √2 represents the square root of 2.
Geometrically, if you have a square with an area of 32 square units, the length of each side of the square will be approximately 4 times the square root of 2 units.
In decimal approximation, the value of √32 is approximately 5.65685.
Exponential Form: 32^½ or 32^0.5
Radical Form: √32 or 4√2
Is the Square Root of 32 Rational or Irrational?
-
Rational numbers are those that can be expressed as a fraction of two integers, where the denominator is not zero. In other words, they can be written in the form a/b, where a and b are integers and b is not equal to zero.
Examples of rational numbers include 1/2, -3, and 5.
- An irrational number is a real number that cannot be expressed as a simple fraction, and its decimal representation goes on infinitely without repeating.Since 32 is not a perfect square, the square root of 32 cannot be expressed as a fraction of two integers. Additionally, the decimal representation of √32 is non-repeating and non-terminating.
Examples of irrational numbers include √2, π (pi), and √3.
- To determine whether √32 is rational or irrational, we check if 32 is a perfect square. Since 32 is not a perfect square, its square root cannot be expressed as a simple fraction. Calculating the square root of 32 yields a non-terminating, non-repeating decimal approximately 5.65685. Since √32 cannot be expressed as a fraction of two integers and its decimal representation is non-repeating and non-terminating, it is classified as an irrational number.
Method to Find Value of Root 32
- Estimation Method:
- Start by finding the nearest perfect squares around 32. In this case, the nearest perfect squares are √25 = 5 and √36 = 6.
- Refine the estimate iteratively using trial and error until you reach a satisfactory approximation.
2. Long Division Method:
- Employ the long division method to approximate the square root of 32 manually.
- Start with an initial guess, such as 5, and proceed with division and adjustment until you achieve the desired accuracy.
- This method involves a series of steps of trial and error to converge on an approximation of √32.
3. Newton’s Method:
- Utilize Newton’s method, an iterative algorithm, to approximate the square root of 32.
- This method involves refining an initial guess through successive iterations until reaching a sufficiently accurate approximation.
- Newton’s method is more efficient but requires a deeper understanding of calculus and iterative algorithms.
4. Using a Calculator or Software:
- The most straightforward method is to use a scientific calculator or mathematical software to directly calculate the square root of 32.
- Input 32 into the calculator or software, and the result will provide the accurate value of √32.
Square Root of 8 by Long Division Method
- Estimation: Begin by estimating the square root of 32. Since 32 is between the perfect squares of 25 (5²) and 36 (6²), you know the square root of 32 should be between 5 and 6.
- Initial Guess: Choose an initial guess between 5 and 6. A good starting point might be 5.5.
- Square Guess: Square your initial guess. Calculate 5.5×5.5 = 30.25.
- Comparison: Compare the squared value (30.25) with 32. Since 30.25 is less than 32, you know you need to adjust your guess upwards.
- Refine Guess: Increase your guess slightly. Let’s try 5.6.
- Square and Compare Again: Square your refined guess. Calculate 5.6×5.6 = 31.36.
- Final Refinement: Repeat the process until you reach a satisfactory approximation. Keep adjusting and comparing until you’re close to 32.
By following these steps iteratively, you can refine your estimate gradually and approach the square root of 32 with increasing accuracy.
32 is Perfect Square root or Not
A perfect square is a number that can be expressed as the square of an integer. In other words, it is the product of an integer multiplied by itself. For example, 25 is a perfect square because it equals 5×5.
However, 32 cannot be expressed as the product of an integer multiplied by itself. Therefore, it is not a perfect square.
FAQ’s
How do you calculate the square root of 32?
There are several methods to calculate the square root of 32, including estimation, long division, Newton’s method, or using a calculator or mathematical software.
How does the square root of 32 relate to other mathematical concepts?
The square root of 32 is related to concepts such as exponentiation, radicals, and quadratic equations, and it finds applications in geometry, algebra, calculus, and other branches of mathematics.
What are the practical applications of the square root of 32?
The square root of 32 has applications in various fields such as mathematics, physics, engineering, finance, and computer science, where precise calculations or measurements are required.
Share :
