What is the square of 35?
1225
1230
1235
1240
of 10
Square & Square Root of 35 – Methods, Calculation, Formula, How to find
Square of 35
The square Numbers of 35, denoted as 35², is calculated by multiplying 35 by itself, resulting in 1225. This value represents the area of a square with sides measuring 35 units each. In various mathematical applications, such as geometry and algebra, the square of 35 is used to determine areas, volumes, and solutions to equations. Understanding the concept and calculation of the square of 35 is fundamental in mathematical reasoning and problem-solving.
Square Root of 35
√35 = 5.91607978309961
or
√35 = 5.916 (rounded to three decimal places)
The square root of 35, denoted as √35, is a value that, when multiplied by itself, equals 35. In simpler terms, it’s the number that, when squared, gives the result 35. While the square root of 35 is not a whole number, it is an irrational number. Mathematically, the square root of 35 is approximately 5.91607978309961. Calculating the square root of 35 involves various methods such as long division, approximation techniques like Newton’s method, or using calculators with square root functions. Understanding the square root of 35 is crucial in mathematics, especially in geometry, algebra, and calculus, where it is used to solve equations and find unknown sides or dimensions in geometric shapes.
Approximate Decimal Form: 5.9160797831
Exponential Form: 35^0.5 or 35¹/²
Radical Form: √35
Is the Square Root of 35 Rational or Irrational?
A rational number is any number that can be expressed as a fraction a/b where a and b are integers, and b is not equal to zero. It includes integers, fractions, and finite or repeating decimals.
An irrational number is a number that cannot be expressed as a simple fraction. Irrational numbers have non-repeating, non-terminating decimal expansions.
This means it cannot be expressed as a fraction of two integers (no matter how large the numbers might be), and its decimal representation goes on infinitely without repeating. Therefore, the square root of 35 is irrational, as it cannot be expressed as a fraction in simplest form, similar to other irrational numbers such as the square root of 21.
Method to Find Value of Root 35
There are several methods to find the square root of 35:
-
Prime Factorization Method:
- Express 35 as a product of its prime factors: 35 = 5 × 7.
- Take one factor from each pair of the prime factors and multiply them: √(5 × 7) = √5 × √7.
- Since 5 and 7 are both prime, their square roots are irrational, so the square root of 35 cannot be simplified further.
-
Estimation Method:
- Start with an initial guess for the square root of 35, such as 6.
- Square this guess: 6² = 36.
- Since 36 is greater than 35, adjust the guess downwards.
- Repeat this process until reaching a satisfactory approximation.
-
Long Division Method:
- Use the long division method similar to polynomial division to calculate the square root of 35 to a desired level of precision.
- This method involves repeatedly subtracting and bringing down digits to approximate the square root.
-
Iterative Methods:
- Utilize iterative algorithms like Newton’s method or the Babylonian method to iteratively refine an initial guess for the square root of 35 until reaching a satisfactory approximation.
Square Root of 35 by Long Division Method
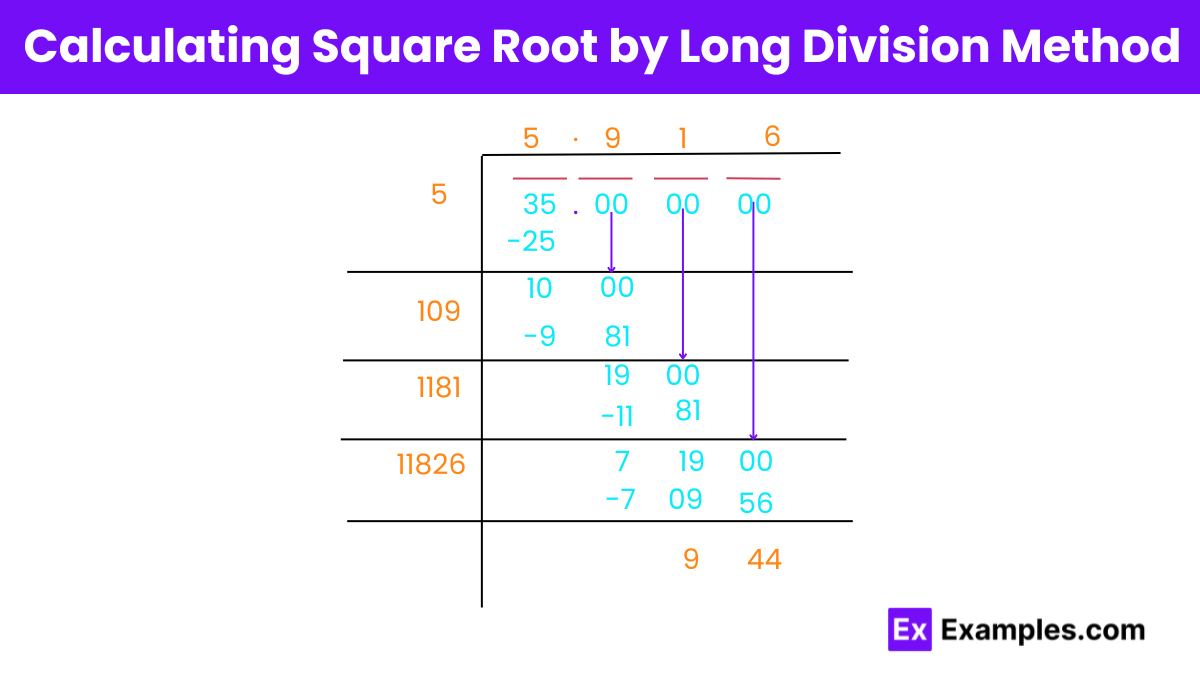
To find the square root of 35 using the long division method, follow these steps:
Set Up the Number: Place the number 35 under the square root sign.
Estimate the Integer Part: Estimate the largest integer whose square is less than or equal to 35. In this case, it’s 5, as 5² = 25.
Divide and Average: Divide 35 by 5, which gives 7. Add the quotient (5) and the divisor (5), then divide by 2 to get the average: (5 + 7) ÷ 2 = 6.
Repeat the Process: Use this average (6) as the next divisor. Divide 35 by 6, which gives approximately 5.833.
Refine the Average: Repeat the process, adjusting the divisor and finding the average until reaching the desired level of accuracy.
Finalize the Result: Continue the process until the decimals repeat or until the desired level of precision is achieved. The resulting quotient provides the decimal approximation of the square root of 35.
Following these steps, the square root of 35, obtained by the long division method, is approximately 5.916.
FAQS
How do you simplify √ 35?
No, we cannot simplify the square root of 35 to an exact whole number.
What two numbers is the square root of 35 between?
The answer is simple: between 5 and 6. The way you find this is you take the nearest perfect square less than 35 and greater than 35. The nearest perfect square less than 35 is 25 and the nearest perfect square greater than 35 is 36.
Share :
Practice Test
Which of the following is closest to the square root of 35?
Which of the following is closest to the square root of 35?
6.0
6.1
6.2
of 10
If x² = 35, what is the value of x?
5.8
5.9
6.0
6.1
of 10
Simplify √35 to its decimal form.
5.8
5.9
6.0
6.1
of 10
What is (35)²?
1200
1215
1225
1235
of 10
Find the approximate value of √35 to two decimal places.
5.90
5.91
5.92
5.93
of 10
Which number is closest to 35 but not a perfect square?
34
36
37
40
of 10
What is 35 raised to the power of 0.5?
5.9
6.0
6.1
6.2
of 10
Calculate 35 × 35.
1200
1225
1250
1275
of 10
What is the square root of 35 rounded to the nearest integer?
5
6
7
8
of 10