Square & Square Root of 42
Square of 42
The square of 42 (42²) is the result of multiplying 42 by itself. So, the square of 42 is 1764.
Geometrically, if you have a square with each side measuring 42 units, the total area enclosed by the square will be 1764 square units.
Understanding the square of 42 is important in various mathematical contexts, including geometry, algebra, and arithmetic. It finds applications in calculating areas, volumes, distances, and solving mathematical problems.
Square Root of 42
or
√72=6.480 up to three places of decimal
The square root of 42 (√42) is an irrational number, approximately equal to 6.480740698. It represents a number that, when multiplied by itself, results in 42. Mathematically,
Since 42 is not a perfect square, its square root cannot be simplified to a whole number or a simple fraction. Instead, it is a non-repeating, non-terminating decimal.
The square root of 42 finds applications in various fields such as mathematics, physics, engineering, and finance, where precise calculations are required.
Exponential Form: 42^½ or 42^0.5
Radical Form: √42
Is the Square Root of 42 Rational or Irrational?
To understand why, let’s delve into the definitions of rational and irrational numbers.
A rational number is any number that can be expressed as a fraction a/b where a and b are integers, and b is not equal to zero. It includes integers, fractions, and finite or repeating decimals.
An irrational number is a real number that cannot be expressed as a simple fraction, and its decimal representation goes on infinitely without repeating.
Since 42 is not a perfect square, its square root cannot be expressed as a fraction of two integers. Additionally, the decimal representation of √42 is non-repeating and non-terminating. Therefore, √42 is classified as an irrational number.
The square root of 42 (√42) is an irrational number. To understand why, consider the definition of rational and irrational numbers. A rational number can be expressed as a simple fraction of two integers, while an irrational number cannot. Since 42 is not a perfect square, its square root cannot be simplified to a fraction. Additionally, the decimal representation of √42 continues infinitely without repeating, indicating its irrational nature. Therefore, the square root of 42 (√42) is classified as an irrational number.
Method to Find Value of Root 42
Estimation Method:
- Start by finding the nearest perfect squares around 42. In this case, the nearest perfect squares are √36 = 6 and √49 = 7.
- Since 42 is closer to 49, start with an initial estimate of √42 ≈ 6.5.
- Refine the estimate iteratively using trial and error until you reach a satisfactory approximation.
Long Division Method:
- Use the long division method to approximate the square root of 42 manually.
- Start with an initial guess, such as 6, and proceed with division and adjustment until you achieve the desired accuracy.
- This method involves a series of steps of trial and error to converge on an approximation of √42.
Newton’s Method:
- Apply Newton’s method, an iterative algorithm, to approximate the square root of 42.
- This method involves refining an initial guess through successive iterations until reaching a sufficiently accurate approximation.
- Newton’s method is more efficient but requires a deeper understanding of calculus and iterative algorithms.
Using a Calculator or Software:
- Utilize a scientific calculator or mathematical software to directly calculate the square root of 42.
- Input 42 into the calculator or software, and the result will provide the accurate value of √42.
Square Root of 42 by Long Division Method
- Digit Pairing: Group the digits from the right side of 42 into pairs. Since we have only one pair (42), put a bar over it.
- Initial Division: Find a number (let’s call it z) such that z × z ≤ 42. Since 6 × 6 = 36 ≤ 42, z is 6. Divide 42 by 6 to get both the quotient and remainder as 6.
- Update Divisor: Add the divisor (6) with itself to get the new divisor (12). This prepares for the next iteration of the division.
- Decimal Placement: Place a decimal point in the quotient part after 6. Also, place 3 pairs of zeros after the decimal in the dividend part.
- Next Pair of Zeros: Bring down one pair of zero from the dividend. The dividend now becomes 600.
- Finding the Next Digit: Find a number (let’s call it m) such that 12m × m ≤ 600. The number m is 4 since 124 × 4 = 496 ≤ 600.
- Repeat Iteration: Repeat the above steps for the remaining two pairs of zeros to continue refining the approximation of the square root of 42.
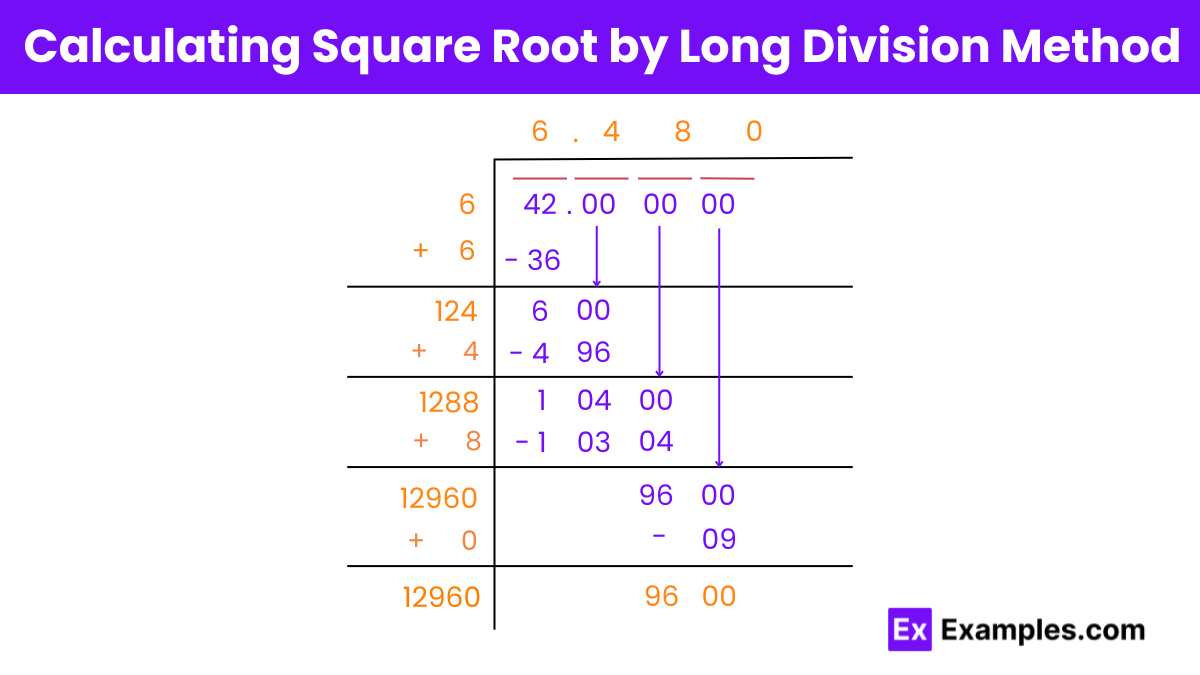
By following this process iteratively, you can refine the approximation of the square root of 42 using the long division method.
42 is Perfect Square root or Not
A perfect square is a number that can be expressed as the square of an integer. In other words, it is the product of an integer multiplied by itself. For example, 25 is a perfect square because it equals 5×5.
However, 42 cannot be expressed as the product of an integer multiplied by itself. Therefore, it is not a perfect square.
FAQ’s
How can I calculate the square root of 42 without a calculator?
Various methods, such as estimation, long division, or using iterative algorithms like Newton’s method, can be used to approximate the value of √42 without a calculator.
What practical applications does the square root of 42 have?
The square root of 42 has applications in fields like mathematics, physics, engineering, and finance, where precise calculations are required. For instance, it might be used in calculating distances, areas, or determining magnitudes of certain quantities.
Can the square root of 42 be expressed in terms of a continued fraction or another mathematical series?
While the square root of 42 can be expressed in terms of a continued fraction or other mathematical series, its representation as an infinite series or continued fraction would provide an alternative way to approximate its value or study its mathematical properties.
Share :
