What is the square of 45?
2025
2075
2100
2200


The “square of 45” refers to the result of multiplying the number 45 by itself. In mathematical terms, it’s represented as 45². To calculate the square of 45, you simply multiply 45 by 45, which equals 2025.
Mathematically, it’s shown as 45² (45×45) = 2025
Understanding how to calculate the square of 45 is straightforward and essential for various mathematical applications, from basic arithmetic to more complex fields like geometry. This process highlights the foundational role of multiplication in forming square numbers and allows us to appreciate the relationship between algebraic expressions and geometric figures.
√45 = 6.708203932499369
or
√45 = 6.708 up to three decimal places
The square root of 45 is the number that, when multiplied by itself, gives the product 45. This concept falls under the broader topic of square root calculation. Finding the square root means you’re searching for a number that, squared, results in 45. This operation is an example of root extraction, which is a basic yet important aspect of algebra.
To calculate the square root of 45, you can use a calculator or apply mathematical methods like estimation or the long division method. The approximate value of the square root of 45 is 6.708, when rounded to three decimal places. This shows the precision involved in finding the square root value.
Understanding how to determine the square root of a number like 45 is useful for a range of mathematical purposes, including solving problems that involve numerical square roots. It illustrates the interesting way numbers can interact through multiplication to reach a given value.
Square root of 45: 6.708203932499369
Exponential Form: 45^½ or 45^0.5
Radical Form: √45
To understand whether the square root of 45 is rational or irrational, let’s first define what rational and irrational numbers are.
Rational numbers are numbers that can be expressed as a fraction or quotient of two integers, where the numerator and denominator are both integers, and the denominator is not zero. In other words, a rational number can be represented as a/b, where (a) and (b) are integers and (b ≠ 0).
Irrational numbers, on the other hand, are numbers that cannot be expressed as a fraction of two integers. These numbers have non-repeating, non-terminating decimal expansions. Classic examples of irrational numbers include π and √2.
Analyzing (√45)
Now, let’s analyze √45. To determine if it’s rational or irrational, we’ll attempt to simplify it:
√45 = √(9 × 5) = √9 × √5 = 3 × √5
Notice that we simplified √45 into 3√45. Here, 3 is a rational number, but what about √5?
√5 is the square root of 5, a prime number. There are no two integers you can multiply together to get exactly 5, meaning √5 cannot be simplified into a fraction of two integers. Therefore, √5 is an irrational number. Since the product of a rational number (3) and an irrational number √5 results in an irrational number, √45 is also irrational.
Conclusion
√45 is an irrational number because it cannot be expressed as a fraction of two integers. Its simplified form, 3 × √5, involves the square root of a prime number (5), which is itself an irrational number. Hence, √45 possesses a non-repeating, non-terminating decimal expansion, characteristic of irrational numbers.
Finding the value of the square root of 45 might seem a bit daunting at first, but it’s actually a straightforward process when you break it down. The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3 because 3 x 3 = 9. So, how do we find the square root of 45, a number that isn’t a perfect square? Let’s explore a few methods.
Estimation Method
One way to find the square root of 45 is through estimation. You know that 6 x 6 = 36 and 7 x 7 = 49. Therefore, the square root of 45 falls between 6 and 7. To get a more precise estimate, you can look at the numbers more closely: since 45 is closer to 49 than it is to 36, its square root is likely closer to 7 than to 6. With a bit of trial and error, you can refine your estimate.
Prime Factorization
Prime factorization involves breaking down 45 into its prime factors. The prime factors of 45 are 3 x 3 x 5, or 3²×5. The square root of 3² is 3, and the square root of 5 remains under the radical because it’s not a perfect square. Therefore, the square root of 45 can be expressed as 3 × √5.
Using a Calculator
For a quick and accurate answer, you can use a calculator. Simply input 45 and press the square root function (usually represented by √). The calculator will give you a decimal approximation of the square root of 45, which is about 6.708.
Decimal Method (Long Division)
The decimal or long division method is a bit more complex and is similar to the traditional long division but tailored for finding square roots. This method involves dividing the number into pairs of digits, estimating the largest possible square, subtracting, bringing down the next pair of digits, and repeating the process to get a decimal approximation of the square root. This method is precise but requires practice and is best for those comfortable with long division.
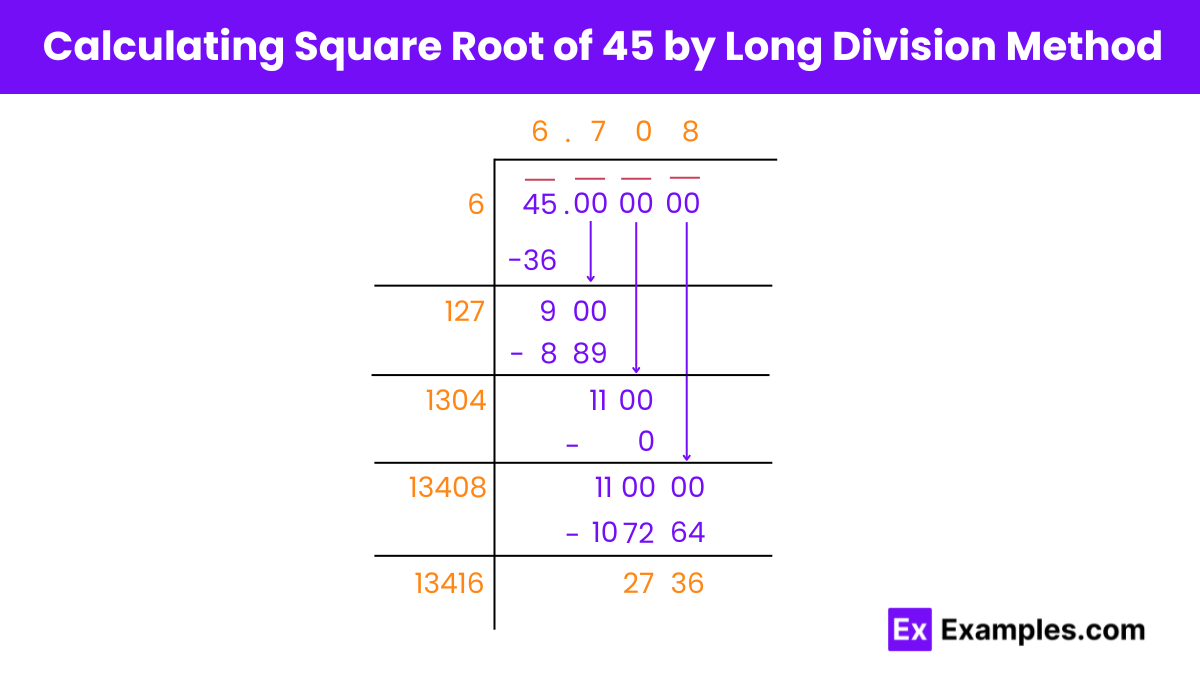
To find the square root of 45 using the long division method, follow these steps:
Step 1: Write 45 in decimal form with six zeros after the decimal point: 45.000000. Pair the digits from right to left, putting a bar on top of the number.
Step 2: Divide 45 by a number so that when squared, the result is less than or equal to 45. We find 6 × 6 = 36, which is less than 45. Therefore, the quotient is 6 and the remainder is 9.
Step 3: Double the quotient to get 12 and assume 120 as the new divisor. Bring down the next pair of zeros to get 900 as the new dividend. Find a number to add to 120 such that the result, when squared, is less than or equal to 900. We find (120 + 7) × 7 = 889, which is less than 900.
Step 4: Subtract 889 from 900 to get 11 as the new remainder and 67 as the new quotient.
Step 5: Double the new quotient to get 134 and assume 1340 as the new divisor. Bring down the next pair of zeros to get 1100 as the new dividend. Find a number to add to 1340 such that the result, when squared, is less than or equal to 1100. We find (1340 + 0) × 0 = 0, which is less than 1100.
Step 6: Subtract 0 from 1100 to get 1100 as the new remainder.
Step 7: Repeat this process until you get the desired level of precision, in this case, three decimal places.
Step 8: Thus, the approximate value of the square root of 45, √45, is 6.708.
To determine if 45 is a perfect square, we need to understand what a perfect square is and then apply that knowledge to the number in question.
What is a Perfect Square?
A perfect square is an integer that can be expressed as the product of an integer multiplied by itself. In other words, it’s the square of an integer. For example, 16 is a perfect square because it can be written as 4² (4 × 4). Similarly, 9 is a perfect square because it can be expressed as 3² (3 × 3).
Determining if 45 is a Perfect Square
To find out if 45 is a perfect square, we need to see if there’s an integer that, when squared, equals 45. The process involves finding the square root of 45 and checking if it is an integer (a whole number without fractions or decimals).
Let’s calculate the square root of 45:
√45
We can either estimate this value or use a calculator for an accurate figure. Let’s compute the exact square root.
The square root of 45 is approximately 6.708. Since this value is not an integer, it indicates that 45 cannot be expressed as the square of an integer. Therefore, 45 is not a perfect square.
The concept of real numbers encompasses a broad spectrum of numerical values, including integers, fractions, decimals, and irrational numbers. The root extraction of 45, denoted as √45, falls within the realm of real numbers. Despite being an irrational number, √45 exists on the number line, situated between other real numbers. This placement underscores its validity as a real number.
To simplify 45 squared, you simply multiply the number 45 by itself. This operation yields the result 2025. The process is straightforward: 45 × 45 = 2025. This value represents the exponentiation of 45, where the number is raised to the power of 2.
Identifying the square root that lies between 45 entails recognizing neighboring square roots on the numerical spectrum. Situated between the square roots of 42 and 49, the square root of 45 occupies a position within this range. Approximating its value, it falls between 6.48 and 7. This numerical range highlights the intermediary position of the square root of 45 amidst other square roots.
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What is the square of 45?
2025
2075
2100
2200
Calculate the square root of 45.
6.5
6.6
6.7
6.8
If 45 is squared, what is the result?
2015
2020
2025
2030
Which of the following is closest to the square root of 45?
6.4
6.5
6.6
6.7
The square of 45 can be expressed as:
2020
2025
2030
2040
Find the approximate value of the square root of 45.
6.5
6.6
6.7
6.8
What do you get when you square 45?
2000
2020
2025
2035
Which number is a good approximation for the square root of 45?
6.6
6.7
6.8
6.9
Determine the square of 45.
2022
2023
2024
2025
Identify the closest integer to the square root of 45.
6
6.5
6.7
7
Before you leave, take our quick quiz to enhance your learning!

