Square & Square Root of 5
Square of 5
To calculate the square number of 5, you simply multiply 5 by itself:
Mathematically, it’s represented as 5 × 5, which equals 25. So, the square of 5 is 25. This is because when you multiply a number by itself, you’re essentially finding the area of a square with side length equal to that number.
Square Root of 5
√5 = 2.23606797749979.
Or
√5 = 2.236. up to three places of decimal
The square root of 5 is a mathematical concept representing a number which, when multiplied by itself, gives the result of 5. In practical terms, it is the length of the side of a square with an area of 5 square units. In summary, the square root of 5 is both a theoretical concept representing the length of a square’s side and a mathematical solution to the equation x²=5, resulting in an irrational number with a decimal representation that extends infinitely without repeating .The square root of 5 can also be represented in exponential form as 5^½
Square Root of 5:2.23606797749979
Exponential Form:5^½
Radical Form:√5
Is the Square Root of 5 Rational or Irrational?
To understand why, let’s delve into the definitions of rational and irrational numbers.
Rational numbers are those that can be expressed as a fraction of two integers, where the denominator is not zero. In other words, they can be written in the form a/b, where a and b are integers and b is not equal to zero.
Examples: 3/4 is a rational number because it can be expressed as the quotient of integers 3 and 4.
Irrational numbers are numbers that cannot be expressed as the quotient or fraction of two integers. They cannot be represented as terminating or repeating decimals. In other words, their decimal representations are non-repeating and non-terminating.
Examples: √2,
- It cannot be expressed as a simple fraction of two integers.
- Its decimal expansion, approximately 2.23606797749979 , goes on infinitely without repeating a pattern.
- The proof of its irrationality involves showing that it cannot be expressed as the quotient of two integers.
Method to Find Value of Root 5
To find the square root of 5, we can use several methods, including estimation, the prime factorization method, and using a calculator. Here, we focus on a simple estimation method for understanding
- Initial Guess: Start with an initial guess for the square root of 5. A reasonable starting point might be 2, since 2×2=4 which is close to 5.
- Iterative Calculation: Apply the iterative formula to refine the guess: xₙ₊₁ =1/2(xₙ +5/xₙ) Here, xₙ₊₁ represents the next approximation of the square root, and xₙ is the current approximation.
- Repeat: Continue iterating by plugging the current approximation into the formula until reaching a satisfactory level of precision or until the difference between consecutive approximations is negligible.
- Convergence: Newton’s method typically converges rapidly, meaning it quickly approaches the actual value of the square root.
- Result: The final value obtained after repeating the process to sufficient accuracy is the value of the square root of 5.
Square Root of 5 by Long Division Method
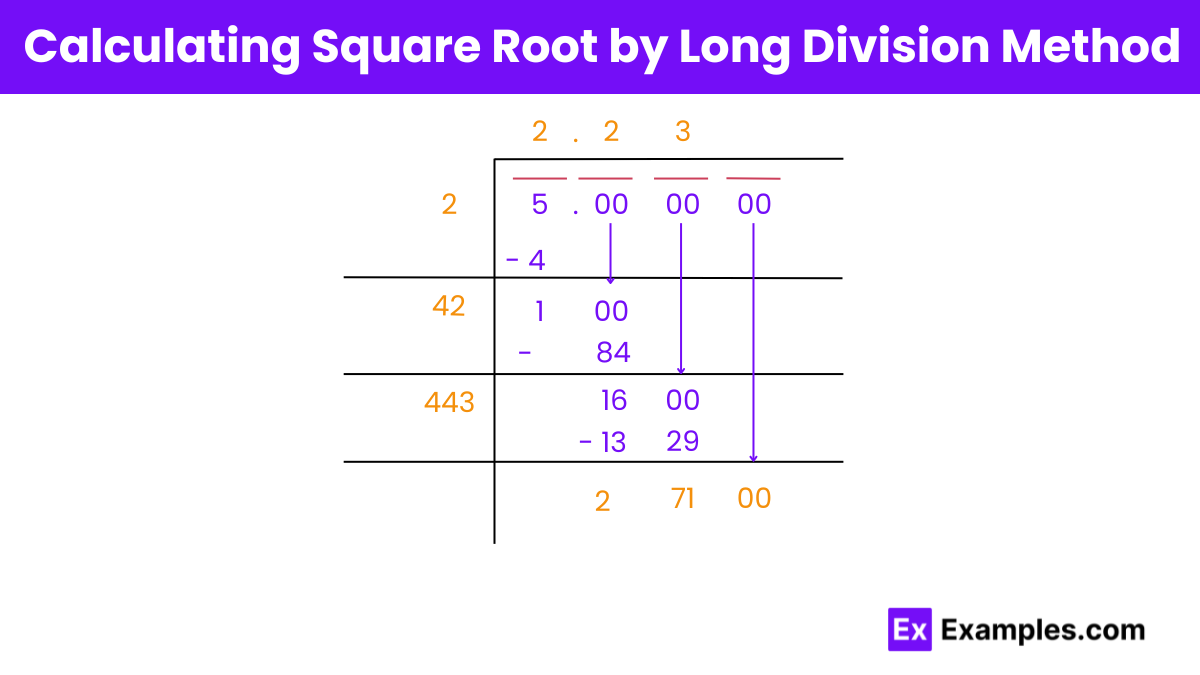
Step 1: Group digits in pairs, starting from the right. Since our number is 5, we place it inside the division symbol.
Step 2: Find the largest number that, when squared, is less than or equal to 5. We find 2 works because 2×2=4, which is less than 5. Divide 5 by 2.
Step 3: Place a decimal point and pairs of zeros, then continue dividing. Multiply the quotient by 2 to get the starting digit of our next divisor.
Step 4: Choose a number in the tens place for the new divisor such that its product with a number is less than or equal to 100. For example, 42 × 2 = 84.
Step 5: Bring down the next pair of zeros and multiply the quotient by 2. This becomes the starting digit of the new divisor.
Step 6: Choose the largest digit in the ones place for the new divisor such that the product of the new divisor with the digit at the ones place is less than or equal to 1600. For example, 443 × 3 = 1329, which is less than 1600.
By following these steps, you can approximate the square root of 5 using the long division method.
Is 5 a Perfect Square root or Not?
The number 5 itself is not a perfect square, but it can be considered a perfect square root if you are asking whether there is a number which, when squared, results in 5. In this case, 5 is the square root of 25, which is a perfect square. However, if the question is about the number 5 itself being a perfect square, the answer is no because there is no integer whose square equals 5.
FAQs Short Question & Answers
Can √5 be simplified?
the square root of 5, denoted as √5, cannot be simplified further because 5 is a prime number and cannot be factored into smaller whole numbers. Therefore, √5 is an irrational number.
Is √ 5 a whole number?
√5 is not a whole number. It is an irrational number because it cannot be expressed as a simple fraction and its decimal representation goes on indefinitely without repeating.
How do you estimate square root of 5?
To find the first perfect square greater than 5, we can start by guessing a number close to the square root of 5, which is approximately 2.2 as you suggested.
Let’s verify if 2.2 is close to the square root of 5 by squaring it:
2.2²=4.84
Since 4.84 is close to 5, our guess of 2.2 for the square root of 5 seems reasonable.
Now, let’s find the first perfect square greater than 5. The next perfect square after 5 is 3²=932=9, which is greater than 5. Therefore, the first perfect square greater than 5 is 9.
Share :
