Square & Square root of 52
Square of 52
The square number of 52 is the result when you multiply 52 by itself. In mathematical terms, it’s represented as 52² or 52×52. When you calculate it, the square of 52 equals 2,704.
Square Root of 52
√52 = 7.21110255093
Or
√52 = 7.211 up to three places of decimal
The square root of 52 is approximately 7.211. This is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation goes on indefinitely without repeating.
Square Root of 52: 7.21110255093
Exponential Form: 52^½
Radical Form: √52
Is the Square Root of 52 Rational or Irrational?
To understand why, let’s break it down:
An irrational number is a number that cannot be expressed as a simple fraction (i.e., the ratio of two integers) and whose decimal representation goes on infinitely without repeating. When we try to find the square root of 52, we find that it doesn’t simplify to a whole number or a fraction. The approximate value of the square root of 52 is around 7.2111. This decimal goes on infinitely without repeating any pattern.
Therefore, because the square root of 52 cannot be expressed as a fraction and its decimal representation is non-repeating and non-terminating, it is considered an irrational number.
Rational numbers In simpler terms, rational numbers are those that can be written as a fraction, where the numerator and denominator are both integers. This includes numbers like 1/2, -3/4, 5/1, and even integers themselves, since they can be expressed as a fraction with a denominator of 1. Rational numbers can be positive, negative, or zero.
Examples: 3/4,−5/2
Irrational numbers are numbers that cannot be expressed as a ratio of two integers, meaning they cannot be written as a simple fraction. These numbers have decimal representations that neither terminate nor repeat. In other words, they have an infinite, non-repeating decimal expansion. Irrational numbers include values such as the square root of non-perfect squares
Examples: √2, √3, √5
- Square of 52: The square of 52 is a rational number, because it’s the result of multiplying 52 by itself, which yields a perfect square: 52²=52×52=2704
- Square root of 52: The square root of 52 is an irrational number because 52 is not a perfect square. It cannot be expressed as the exact quotient of two integers. However, we can approximate its value using decimal notation:√ 52≈7.21110255093.
- Representation: The square of 34 can be represented as 52²=2704, while the square root of 52 can be represented as √52.
Methods to Find Value of Root 52
Prime Factorization: Start by finding the prime factorization of 52. 52=2×2×13
Pair the Factors: Group the prime factors in pairs. Since there are two 2’s, we can take one out of the radical and leave one inside. √52 = √2×2×13=2 √13
Estimate: First, estimate the square root of 52. Since 52 is between the perfect squares 49 (7 squared) and 64 (8 squared), you can estimate that the square root of 52 is somewhere between 7 and 8.
Newton’s Method: (Iterative Method): Newton’s method is an iterative method used to approximate roots of functions. For the square root, the formula is:
Xₙ₊₁ = 1/2(Xₙ+ 52/Xₙ)
Let’s start with X₀=7.5
Substitute X₀ into the formula:
X₁ = 1/2(7.5+52/7.5)
X₁ = 1/2(14.4333)
X₁≈ 7.21665
Square Root of 52 by Long Division Method
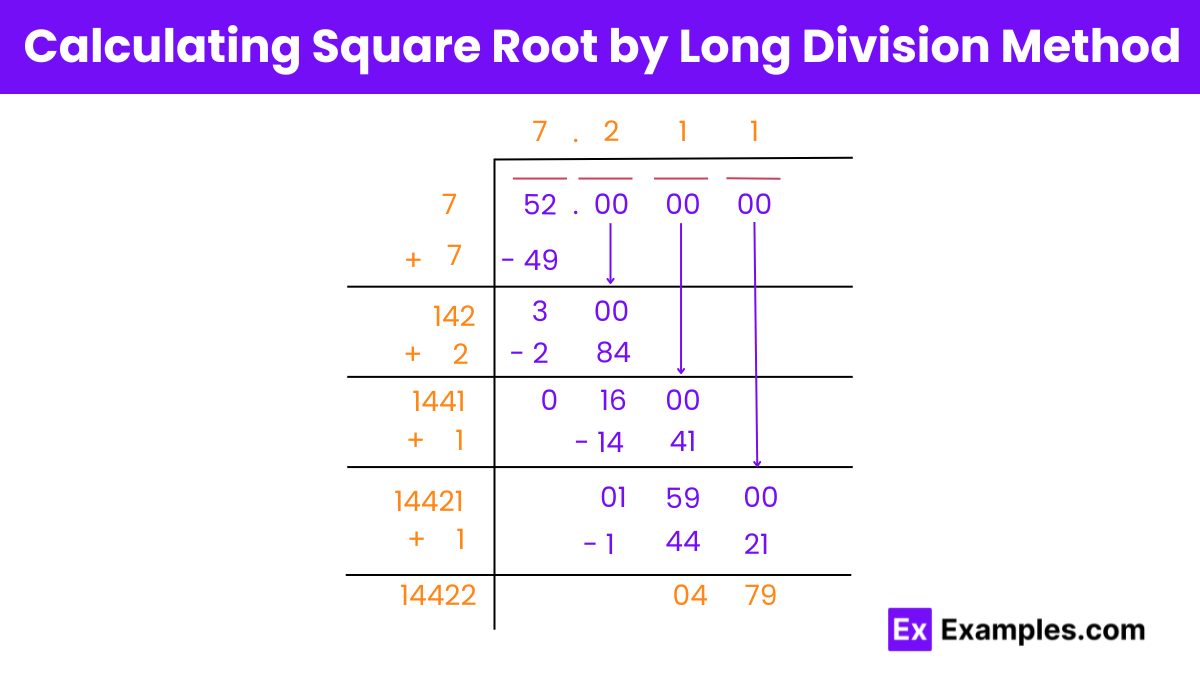
Finding the square root of 52 using the long division method involves a step-by-step process that is somewhat similar to the traditional division method we use for numbers. Here’s a simplified explanation of how it works:
Step 1: Set Up the Problem
Write down the number 52, and pair the digits from right to left. In this case, we only have two digits, so it’s already paired. It will look something like this: 52.
Step 2: Find the Largest Square
Find the largest square less than or equal to 52. Since
7²=49 and
8²=64, we know that 7 is the largest whole number whose square is less than or equal to 52. So, we place 7 above the line, and 49 below 52, because
7² =49
Step 3: Subtract and Bring Down
Subtract 49 from 52, which gives us 3. Since there are no more digits to bring down, we add a decimal point and pairs of zeros to continue the division. It now looks like 300.
Step 4: Double the Quotient
Double the current quotient (which is 7), making it 14. Now, we need to find a digit (let’s call it “X”) that fits in the equation 14X×X≤300. The value of X must be such that when you add it to 14 and then multiply by the same digit, the product is less than or equal to 300.
Step 5: Find the Next Digit
Start with 1; 141×1=141, which is less than 300. If we try 2, 142×2=284, which is still less than 300. But if we try 3, 143×3=429, which is too high. So, the next digit is 2.
Step 6: Repeat the Process
Place the 2 next to the 7 in the quotient, making it 7.2. Subtract 142×2=284 from 300 to get 16, and bring down another pair of zeros to continue the division, making it 1600.
Now, double the current quotient (ignoring the decimal) which gives 72×2 = 144, and find the next digit in the same way as step 4 and 5.
This process can be repeated to get as many decimal places as you need.
Is 52 a Perfect Square root or Not?
No, A perfect square is a number that is the square of an integer. There are no integers that, when squared, result in 52. The square root of 52 is an irrational number, approximately 7.211, which confirms that 52 is not a perfect square.
FAQs Short Question & Answers
Is 52 a perfect square?
is not a perfect square. A perfect square is a number that can be expressed as the product of an integer with itself. For example, 49 is a perfect square because it is 7 times 7. The nearest perfect squares to 52 are 49 (7 x 7) and 64 (8 x 8), but 52 cannot be expressed as the square of an integer.
What are the factors of 52?
The factors of 52 are the numbers that you can multiply together to get 52. These include:
- 1 and 52, because 1 x 52 = 52
- 2 and 26, because 2 x 26 = 52
- 4 and 13, because 4 x 13 = 52
So, the factors of 52 are 1, 2, 4, 13, 26, and 52.
Is 52 a composite number?
52 is a composite number. A composite number is a positive integer that has at least one positive divisor other than one or itself. In other words, a composite number is any positive integer greater than 1 that is not a prime number. Since 52 has divisors other than 1 and itself (for example, 2, 4, 13, and 26), it is considered a composite number.
Does 52 have two factors?
52 has more than two factors. As mentioned earlier, the factors of 52 are 1, 2, 4, 13, 26, and 52. This list shows that 52 has six factors, not just two. A number with exactly two factors, 1 and itself, is known as a prime number, and 52 does not fit this definition since it has additional factors beyond just 1 and 52
Share :
