Square & Square root of 56
Square of 56
To calculate the square number of 56, you simply multiply 56 by itself:
Therefore, the square of 56 is 3136. This straightforward calculation is a building block for more complex mathematical operations and concepts, including algebraic equations, geometric formulas, and statistical models.
Square Root of 56
Or
√56 = 7.483
The square root of 56, denoted as √56, equals approximately 7.48. To compute it, you find the number that, when multiplied by itself, results in 56. In mathematical terms, finding the square root means identifying the number that, when raised to the power of 2, equals the original number. Visually, you can represent the square root of 56 as one side of a square with an area of 56 square units, where each side of the square is approximately 7.48 units in length. Understanding square roots is fundamental in various mathematical concepts and applications, such as geometry, algebra, and solving problems that involve areas or other quantities that are squared. In real-world scenarios, knowing the square root of 56 aids in calculations involving the measurement of areas or in any situation where you need to reverse a squaring operation to find an original quantity.
Square Root of 56: 7.483314774
Exponential Form: 56^1/2 or 56^0.5
Radical Form: √56
Is the Square Root of 56 Rational or Irrational?
An irrational number cannot be expressed as a simple fraction or a precise decimal; it goes on infinitely without repeating. Since 56 is not a perfect square, its square root cannot be simplified into a fraction that perfectly represents a ratio of two integers, making it an irrational number.
Rational numbers can be written as a fraction with both the numerator and denominator as integers, where the denominator is not zero.
Examples:1/2, 3/4
Irrational numbers cannot be written as simple fractions and their decimal forms do not repeat or terminate.
Examples:π and √22
Methods to Find Value of Root 56
1. Trial and Error
This method involves guessing a number that, when squared, comes close to 56. Start with numbers you know the squares of (e.g., 7² = 49 and 8² = 64) and estimate that √56 falls between 7 and 8.
2. Long Division Method
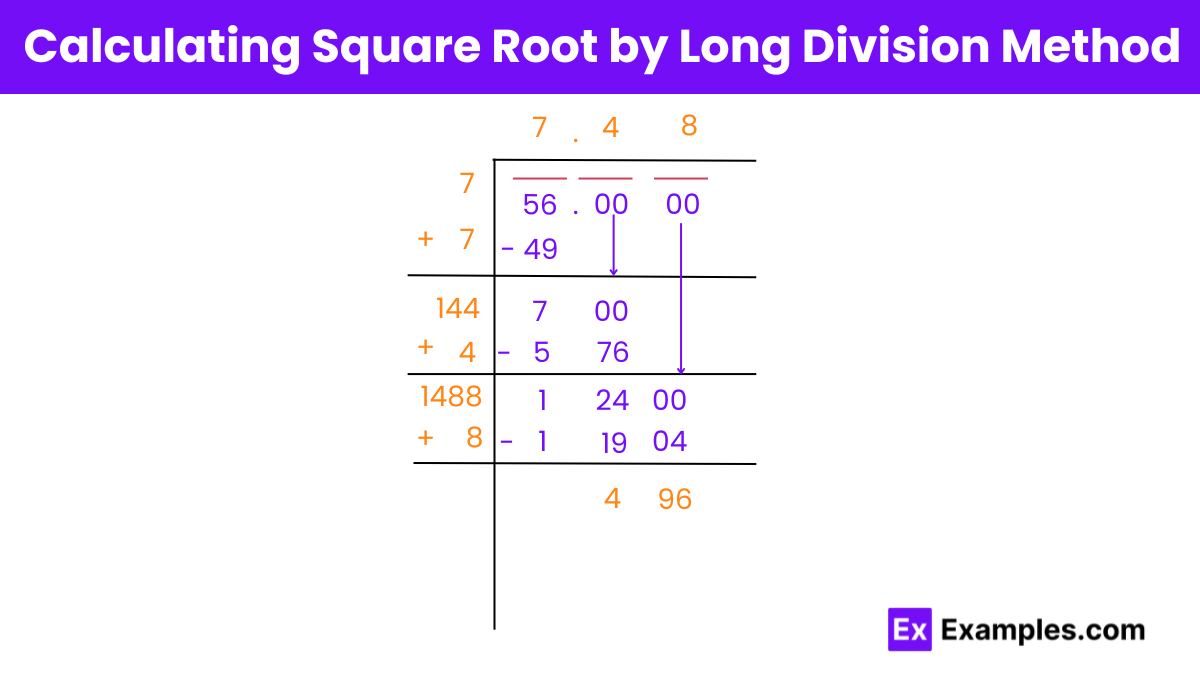
The long division method is a step-by-step procedure similar to traditional division, tailored for finding square roots. It involves dividing the number into pairs of digits from right to left, guessing the largest possible digits whose square is less than or equal to each segment, and subtracting to proceed to the next step. This method is precise but requires practice to master.
3. Prime Factorization
Prime factorization involves breaking down 56 into its prime factors (56 = 2 x 2 x 2 x 7) and then taking the square root of each factor. Since √56 = √(2² x 2 x 7), and knowing that the square root of a square is the number itself (i.e., √(2²) = 2), we simplify it to 2√14, acknowledging that √14 is irrational.
4. Using a Calculator
For most practical purposes, using a scientific calculator is the quickest and easiest way to find the square root of 56. It provides an approximate decimal value, which is sufficient for most applications.
5. Approximation Techniques
Approximation techniques involve using known square roots of perfect squares close to 56 and then estimating or using a formula to get closer to the exact square root. For example, knowing that √49 = 7 and √64 = 8, one can estimate √56 to be closer to 7.5.
6. Newton’s Method
Newton’s Method, or the Newton-Raphson method, is a powerful technique for finding increasingly accurate approximations to the roots (or zeroes) of a real-valued function. To find √56, you would start with an initial guess and iteratively apply Newton’s formula: xₙ₊₁ = xₙ – (f(xₙ)/f'(xₙ)), where f(x) = x² – 56. This method requires knowledge of calculus and is very effective for finding square roots to a high degree of accuracy.
Square Root of 56 by Long Division Method
- Start with an Estimate: Since 7² is 49 and close to 56, divide 56 by 7. The quotient is 7, which is also our divisor.
- Initial Subtraction: Multiply the quotient (7) by the divisor (7) to get 49. Subtract this from 56 to start.
- Double the Quotient: Add the quotient (7) to itself (7 + 7).
- Introduce Decimals: Put a decimal after the quotient (7) and bring down two zeros to make it 700. Now, find a number that, when added to the end of 14 (from step 3) and multiplied by itself, gives a result under 700. Using 4 gives us 576. Subtract this from 700 to continue.
- Bring Down More Zeros: Add two more zeros to the remainder to get 12400. Increase the divisor (now 144) by the digit found in step 4 (4) to get 148. Find a digit that, when added to the end of 148 and multiplied, gives a number less than 12400. With 8, we get 11904. Place this digit after the decimal in the quotient and subtract to find the new remainder.
- Repeat as Needed: Continue the process, bringing down zeros and finding digits until the remainder is zero or you reach the desired decimal places.
is 56 Perfect Square root or Not
A perfect square is a number that can be expressed as the square of an integer. Since there is no whole number that, when multiplied by itself, equals 56, it is not considered a perfect square.
FAQ’S
What is square root of 56 simplified?
The square root of 56 simplified is √56 or approximately 7.48. It’s an irrational number, so it cannot be expressed as a simple fraction.
How do you work out 56 squared?
To work out 56 squared, multiply 56 by itself: 56 × 56 = 3136. This operation calculates the square of 56.
Which number is closest to √56?
The number closest to √56 is 7, as √56 is approximately 7.48. Seven is just slightly less than the actual square root, making it the nearest whole number.
Share :
