What is the square of 61?
3721
3061
2521
4621

To calculate the square of 61, you simply multiply 61 by itself:
The square of 61 (61²) is the result of multiplying 61 by itself. In mathematical terms, 61 squared equals 3721.
Geometrically, this means that if you have a square with each side measuring 61 units, the total area enclosed by the square will be 3721 square units.
Understanding the square of 61 is important in various mathematical contexts, including geometry, algebra, and arithmetic. It’s a fundamental operation that finds applications in numerous real-world scenarios, such as calculating areas, volumes, distances, and solving mathematical problems
√61 = 7.81025
or
√61=7.810 up to three places of decimal
The square root of 61 (√61) is approximately 7.81025.
Similar to the square root of 30, the square root of 61 is also an irrational number, which means it cannot be expressed as a simple fraction, and its decimal representation goes on infinitely without repeating.
Mathematically, √61 represents a number that, when multiplied by itself, equals 61. However, since 61 is not a perfect square, its square root is an irrational number. The approximate value of √61 is around 7.81025. This value can be computed using various numerical approximation methods, such as long division, Newton’s method, or using a calculator or computer software.
In practical applications, the square root of 61 might be encountered in various fields such as mathematics, physics, engineering, finance, and geometry, where precise measurements or calculations are necessary.
Square Root of 61:7.81025
Exponential Form: 61^½ or 61^0.5
Radical Form: √61
Similar to the explanation for the square root of 24, the square root of 61 cannot be expressed as a simple fraction of two integers. Its decimal representation is non-terminating and non-repeating, which classifies it as an irrational number. The approximate value of √61 is around 7.81024967591.
Understanding the square root of 61 is essential in various mathematical contexts, including geometry, algebra, engineering, and physics, where precise calculations and understanding of spatial relationships are required.
There are several methods to approximate the value of the square root of 61. Here are a few common ones:
1.Long Division Method: This is a manual method where you perform long division to approximate the square root. It involves repeatedly subtracting perfect square numbers from the given number and bringing down pairs of digits until you achieve the desired level of accuracy.
2.Newton’s Method: Also known as the Newton-Raphson method, it’s an iterative numerical method for finding the roots of a real-valued function. It involves repeatedly applying a simple formula to refine the approximation until the desired level of accuracy is achieved.
3.Using a Calculator or Software: Most calculators and mathematical software have built-in functions to compute square roots accurately. You can simply input √61 into a calculator or use a mathematical software package to find the approximate value.
4.Binomial Expansion: This method involves using the binomial expansion theorem to expand the square root expression into a series. By truncating the series at a certain point, you can obtain an approximation for the square root.
5.Approximation with Known Square Roots: You can approximate √61 by finding the nearest perfect squares (such as √49 and √64) and then linearly interpolating between them to get a rough estimate.
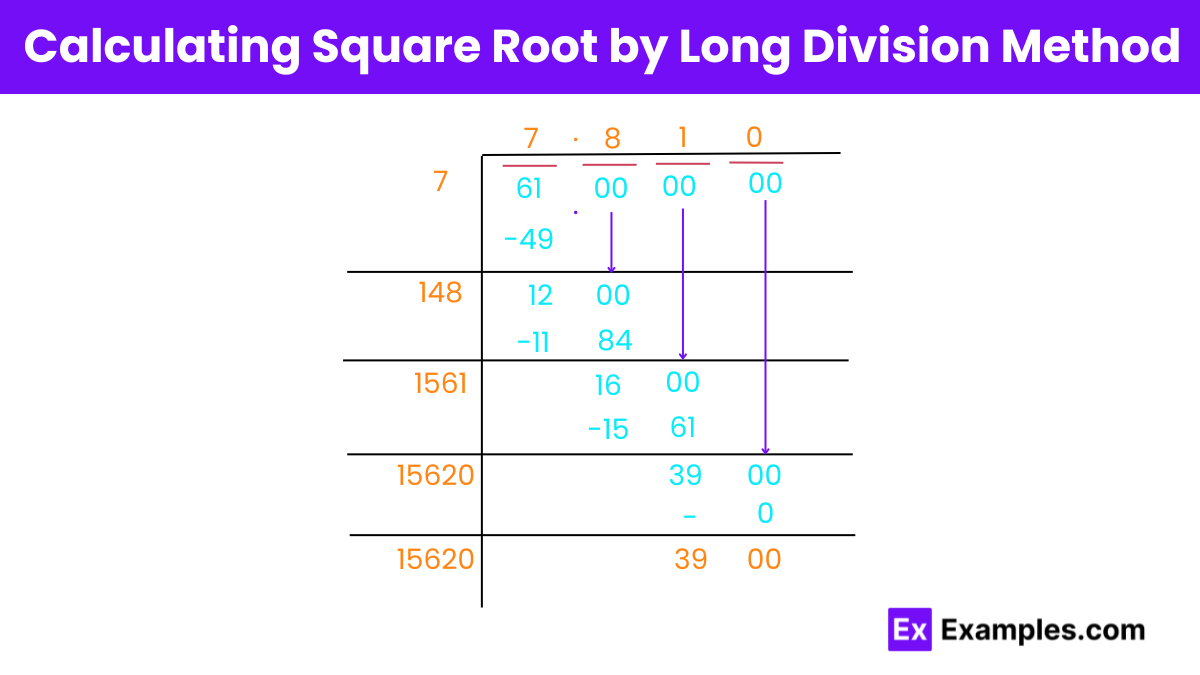
Step 1: Start with the Number: Think of the number 61. We want to find which number, when multiplied by itself, gives a result close to 61 without going over.
Step 2: Initial Guess: Start by finding a simple square number less than or equal to 61. The closest one is 49, which is 7 squared (7×7=49). So, our first guess is 7.
Step 3: Subtract and Bring Down: Subtract 49 from 61, which gives us 12. This is our remainder. In the long division method, we would normally “bring down” the next digits, but since there are none, we can start adding decimal places to 61, treating it as 6100, 610000, and so on, for more precision.
Step 4:Refine Your Guess: Double your current guess (7×2=14) and write it down with a space for a new digit (14_). This is your new divisor. Now, you need to find a digit to put in the blank that, when added to 14_, gives a product less than or equal to your current dividend (in the first step, this is 1200, because we’re treating the remainder 12 as 1200 for more precision). This digit is also your new quotient digit.
Step 5:Repeat for Precision: Subtract the product of your new divisor and the new digit from the dividend, get the new remainder, and repeat the process for as many decimal places as you want. Each time, you’re doubling the entire current quotient (ignoring the decimal) for the new divisor, guessing a digit to complete it, and checking if the product is less than the current dividend.
Step 6: Continue Until Satisfied Keep repeating the process, adding pairs of zeros and calculating subsequent digits of the square root. You can continue this for as many decimal places as you require.
A perfect square is a number that can be expressed as the product of an integer with itself. For example, 4, 9, 16, and 25 are perfect squares because they can be expressed as 2×2, 3×3, 4×4, and 5×5 respectively.
However, the square root of 61 is an irrational number because it cannot be expressed as the ratio of two integers, and its decimal representation goes on infinitely without repeating any pattern. The approximate value of √61 is approximately 7.81024967591.
The number 61 is a prime number. This implies that the number 61 is pairless and is not in the power of 2. Therefore, the radical form of square root of 61 cannot be simplified further.
The square root of 8 is 64, the square root of 7 is 49. 61 is closer to 64. Integers cannot be fractions, so the answer of 7.8 is rounded up to 8!
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What is the square of 61?
3721
3061
2521
4621
What is the approximate square root of 61?
7.81
8.00
7.00
6.50
Which of the following is true about the square of 61?
It is greater than 3600.
It is less than 3600.
It is equal to 3600.
It is less than 4000.
If you take the square root of 61 and square it, what do you get?
61
1
0
21
What is the closest integer to the square root of 61?
7
8
9
10
What is the square of the square root of 61?
61
7.81
8
3721
How much is the square of 61 less than 4000?
279
200
500
300
What is the difference between the square of 61 and 3600?
121
1219
111
180
Which of these values is a perfect square close to 61?
60
62
64
68
What is the approximate value of the square root of 61 rounded to two decimal places?
7.81
7.80
7.90
8.00
Before you leave, take our quick quiz to enhance your learning!

