Square & Square Root of 64
Square of 64
To calculate the square of 64, you multiply 64 by itself:
Thus, the square of 64 is 4096. This process involves taking 64 and multiplying it by 64 once again, yielding a product of 4096. Squaring a number is a basic mathematical operation with applications in various fields, including geometry, physics, and finance, to name a few.
Square Root of 64
√64 = 8
The square root of 64 is a rational number, and it can be expressed precisely as an integer. The square root of 64 is 8. This is because 8 multiplied by itself (8 × 8) equals 64. The square root function essentially asks, “What number, when multiplied by itself, gives the original number?” For 64, that number is 8.
This concept is foundational in many areas of mathematics and its applications, such as geometry, where it might represent the side length of a square with an area of 64 square units, or in algebra and physics, where it helps in simplifying equations and understanding various phenomena.
Square Root of 64: 8
Exponential Form: 64^½ or 64^0.5
Radical Form: √64
Is the Square Root of 64 Rational or Irrational?
A rational number is basically any number that you can write as a fraction, where both the top number (numerator) and the bottom number (denominator) are whole numbers. For example, 1/2 is a rational number because it’s a simple fraction. Now, when we take the square root of 64, we get 8. Since 8 can be written as 8/1 (eight over one), it fits the bill of being a fraction with whole numbers on the top and bottom, making it a rational number.
Understanding whether a number is rational or irrational can sometimes seem a bit tricky, especially with square roots. But it helps to remember that if the square root gives you a clean, whole number or a fraction that doesn’t go on forever, then it’s rational. In the case of the square root of 64, the answer is exactly 8, with no messy, never-ending decimal in sight. That’s why we can confidently say the square root of 64 is a nice, neat rational number, easy to understand and work with in all sorts of math problems.
Methods to Find Value of Root 64
1.Basic Multiplication Knowledge: Since the square root operation asks, “Which number multiplied by itself gives 64?”, you can rely on basic multiplication facts. You might recall that 8 multiplied by 8 equals 64. Therefore, the square root of 64 is 8. This method is quick and relies on memorized multiplication tables.
2.Prime Factorization: This method involves breaking down the number 64 into its prime factors. The prime factorization of 64 is 2 × 2 × 2 × 2 × 2 × 2, since 64 is a power of 2 (2^6). To find the square root, you pair up the prime factors and take one from each pair. Since all the prime factors of 64 are 2, pairing them gives us three pairs of 2s. Taking one number from each pair, we have 2 × 2 × 2, which equals 8. Therefore, the square root of 64 is 8.
Both of these methods will lead you to the same conclusion: the square root of 64 is 8, which is a straightforward and exact value, reflecting the simplicity of working with powers of 2.
Square Root of 64 by Long Division Method
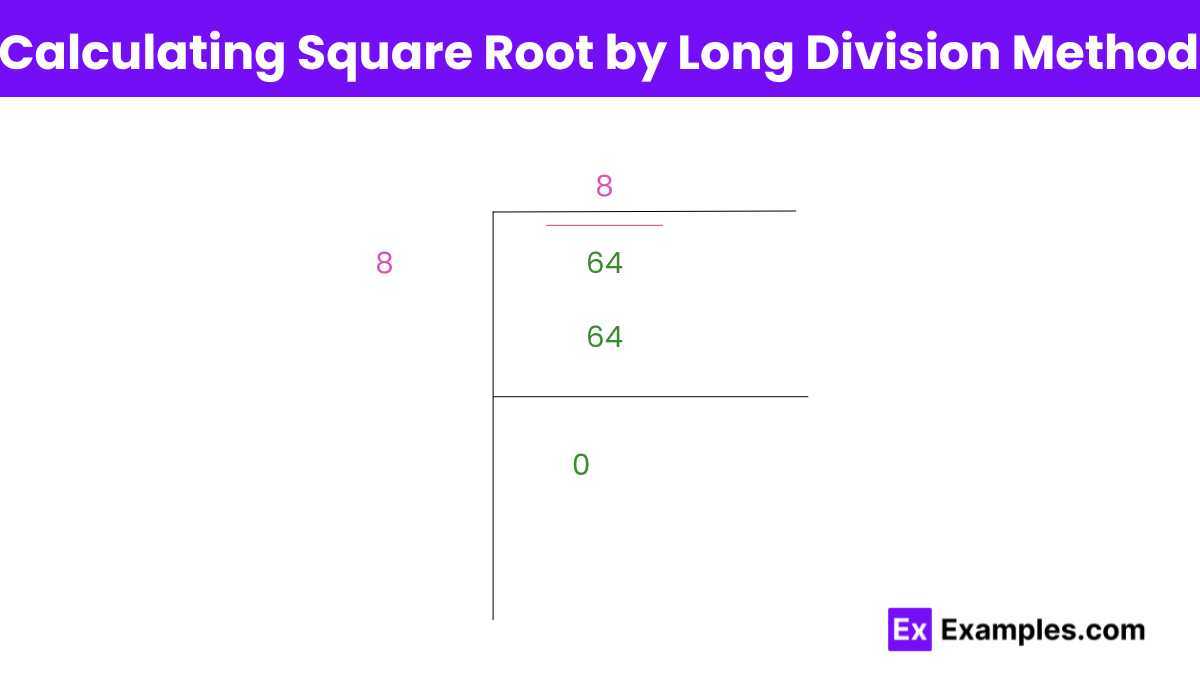
Finding the square root of 64 using the long division method is a systematic approach that might seem a bit elaborate for a number like 64, whose square root is a simple integer (8). However, it’s a great exercise to understand how the method works, especially for numbers that don’t have such straightforward square roots. Here’s a simplified explanation:
Step 1: Set Up the Number: Write 64 under a square root sign. Since 64 is a two-digit number, you don’t need to pair digits from the right as you might with larger numbers.
Step 2: Initial Guess: Think of a number that, when squared, gives a value less than or equal to 64. In this case, it’s easy: 8 × 8 = 64.
Step 3:Subtract and Bring Down: Write 8 outside the square root sign, as your initial guess. Multiply 8 by 8, and write 64 below the original 64. Subtract to get a remainder of 0. Since there are no more digits to bring down, the process technically stops here for whole numbers like 64.
Step 4: Repeat if Necessary: For numbers that don’t have perfect square roots, you would add decimal places (by adding zeros in pairs) and continue the process, making guesses, subtracting, and bringing down digits until you reach the desired level of precision.
For 64, the long division method quickly reveals that 8 is the square root, as 8 times 8 precisely equals 64, leaving no remainder. This straightforward case illustrates the process but also shows why the long division method is often reserved for more complex square roots, where the answer isn’t an obvious integer.
64 is Perfect Square root or Not?
A perfect square is a number that you can get by multiplying an integer (a whole number, like 1, 2, 3, and so on) by itself. For example, 1 is a perfect square because 1 × 1 = 1, and 9 is a perfect square because 3 × 3 = 9.
Now, when it comes to 64, it fits this pattern because there’s an integer, 8, that when multiplied by itself, gives 64 (8 × 8 = 64). Since we found an integer that can be squared to get 64, that makes 64 a perfect square. It’s “perfect” because the multiplication involves no fractions or decimals; it’s a neat and tidy whole number.
FAQ’s
Is 64 a square or cube?
64 is a perfect square of 8. 64 is a perfect cube of 4. Now the next perfect square is the square of 9 which is 81.
Share :
