Square & Square Root of 70 – Methods, Calculation, Formula, How to find
Square of 70
The square of 70 (70²) is calculated by multiplying 70 by itself:
70×70=4900.
So, the square of 70 is 4900.
Geometrically, if you have a square with each side measuring 70 units, the total area enclosed by the square will be 4900 square units.
Understanding the square of 70 is essential in various mathematical contexts, including geometry, algebra, and arithmetic. It finds applications in calculating areas, volumes, distances, and solving mathematical problems.
Square Root of 70
or
√70= 8.366 up to three places of decimal
The square root of 70 (√70) is an irrational number, approximately equal to 8.36660026534.
It represents a number that, when multiplied by itself, results in 70:
70≈8.3666002653470≈8.36660026534
Since 70 is not a perfect square, its square root cannot be simplified to a whole number or a simple fraction. Instead, it is a non-repeating, non-terminating decimal.
The square root of 70 finds applications in various fields such as mathematics, physics, engineering, and finance, where precise calculations are required.
Exponential Form: 70^½ or 70^0.5
Radical Form: √70
Is the Square Root of 70 Rational or Irrational?
The square root of 70 is an irrational number. This can be understood by breaking down what rational and irrational numbers are:
- A rational number is any number that can be expressed as a fraction a/b where a and b are integers, and b is not equal to zero. It includes integers, fractions, and finite or repeating decimals.
- An irrational number is a real number that cannot be expressed as a simple fraction, and its decimal representation goes on infinitely without repeating.
Since 70 is not a perfect square, its square root cannot be expressed as a fraction of two integers. Additionally, the decimal representation of √70 is non-repeating and non-terminating. Therefore, √70 is classified as an irrational number.The square root of 70 (√70) is irrational because it cannot be expressed as a simple fraction, and its decimal representation goes on infinitely without repeating. This is because 70 is not a perfect square, meaning it cannot be expressed as the product of an integer multiplied by itself. The square root of 70 (√70) is classified as an irrational number.
Methods to Find Value of Root 70
Estimation Method:
- Start by finding the nearest perfect squares around 70. In this case, the nearest perfect squares are √64 = 8 and √81 = 9.
- Since 70 is closer to 64, start with an initial estimate of √70 ≈ 8.5.
- Refine the estimate iteratively using trial and error until you reach a satisfactory approximation.
Long Division Method:
- Use the long division method to approximate the square root of 70 manually.
- Start with an initial guess, such as 8, and proceed with division and adjustment until you achieve the desired accuracy.
- This method involves a series of steps of trial and error to converge on an approximation of √70.
Newton’s Method:
- Apply Newton’s method, an iterative algorithm, to approximate the square root of 70.
- This method involves refining an initial guess through successive iterations until reaching a sufficiently accurate approximation.
- Newton’s method is more efficient but requires a deeper understanding of calculus and iterative algorithms.
Using a Calculator or Software:
- Utilize a scientific calculator or mathematical software to directly calculate the square root of 70.
- Input 70 into the calculator or software, and the result will provide the accurate value of √70.
Square Root of 70 by Long Division Method
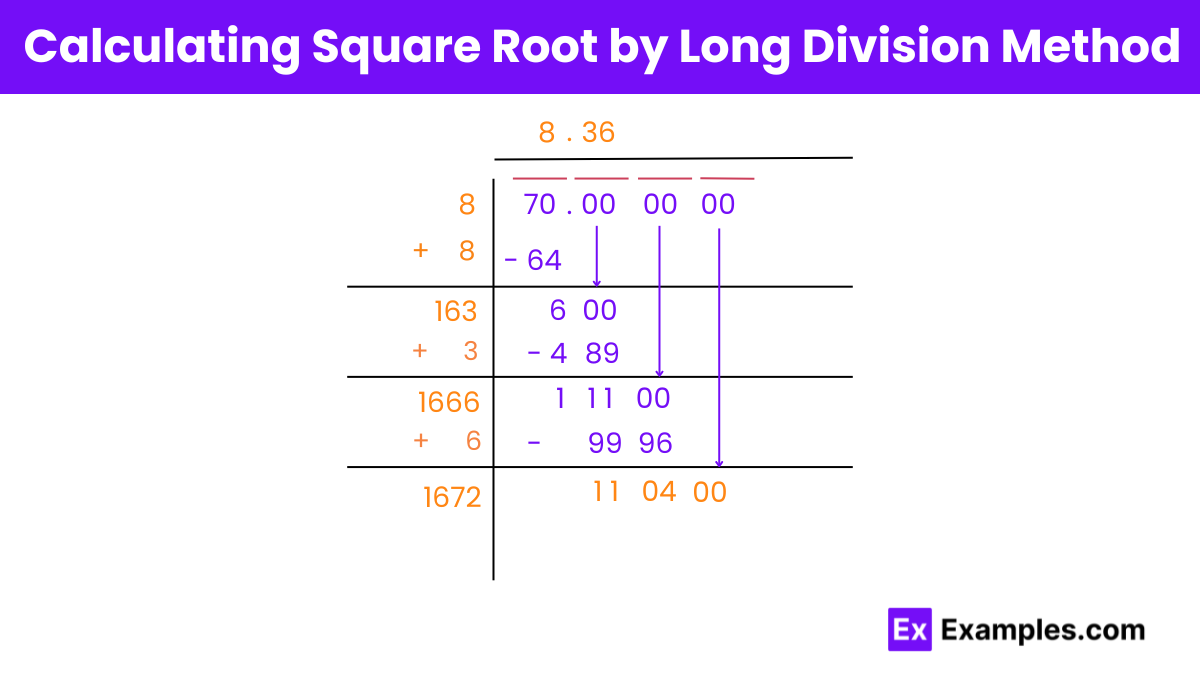
- Pairing Digits: Pair up the digits of 70, starting from the right, and place a bar above them. Also, group the decimal zeros in pairs from left to right.
- Initial Division: Find a number that, when squared, gives a product less than or equal to 70. In this case, 8 fits as 8×8 = 64. Divide 70 by 8, with the quotient and remainder both as 8 and 6, respectively.
- Adding Zero Pairs: Bring down a pair of zeros next to the remainder 6, making the dividend 600.
- Doubling the Divisor: Double the divisor 8 to get 16, and write it below with a blank space on its right. Guess the largest possible digit (X) to fill in the blank, making the product 16X×X less than or equal to 600. In this case, X is 3, resulting in 163.
- Iterative Process: Repeat the process to obtain the desired number of decimal places for the square root of 70.
70 is Perfect Square root or Not
FAQ’s
What practical applications does the square root of 70 have?
The square root of 70 has applications in fields like mathematics, physics, engineering, and finance, where precise calculations are required. For instance, it might be used in calculating distances, areas, or determining magnitudes of certain quantities.
How can I calculate the square root of 70 without a calculator?
Various methods, such as estimation, long division, or using iterative algorithms like Newton’s method, can be used to approximate the value of √70 without a calculator.
Are there any interesting mathematical properties of the number 70 related to its square root?
While the number 70 has various interesting mathematical properties, such as being a product of two prime numbers (2×5×7), its square root’s properties are more closely related to general properties of square roots and irrational numbers.


