What is the approximate square root of 80?
8.6
8.7
8.8
8.9

To calculate the square of 80, you simply multiply 80 by itself:
Therefore, the square of 80 is 6400. This straightforward calculation is a building block for more complex mathematical operations and concepts, including algebraic equations, geometric formulas, and statistical models.
The square root of 80, denoted as √80, equals approximately 8.94. To compute it, you find the number that, when multiplied by itself, results in 80. In mathematical terms, finding the square root means identifying the number that, when raised to the power of 2, equals the original number. Visually, you can represent the square root of 80 as one side of a square with an area of 80 square units, where each side of the square is approximately 8.94 units in length. Understanding square roots is fundamental in various mathematical concepts and applications, such as geometry, algebra, and solving problems that involve areas or other quantities that are squared. In real-world scenarios, knowing the square root of 80 aids in calculations involving the measurement of areas or in any situation where you need to reverse a squaring operation to find an original quantity.
Exponential Form: 80^1/2 or 80^0.5
Radical Form: √80
An irrational number is one that cannot be expressed as a simple fraction (a ratio of two integers). The square root of 80, when simplified, is √80=√16×√5=4√5. Since √5 is not a perfect square and its decimal form is non-terminating and non-repeating, it cannot be expressed as a fraction of two integers. Therefore, 4√5 (and thus, the square root of 80) is irrational, as it cannot be precisely represented as a fraction.
Finding the value of the square root of 80 can be approached in several ways, depending on the level of precision you need and the tools you have available. Here are some methods:
1. Using a Calculator
The simplest and most accurate method to find the square root of 80 is to use a calculator. Just enter “80” followed by the square root function (√), and it will give you the precise value, which is approximately 8.94427.
2. Estimation
If you don’t have a calculator handy, you can estimate the square root of 80 by identifying the perfect squares closest to it, which are 64 (8²) and 81 (9²). Since 80 is closer to 81, you know that the square root of 80 is slightly less than 9.
3. Prime Factorization
You can also use prime factorization to simplify the square root:
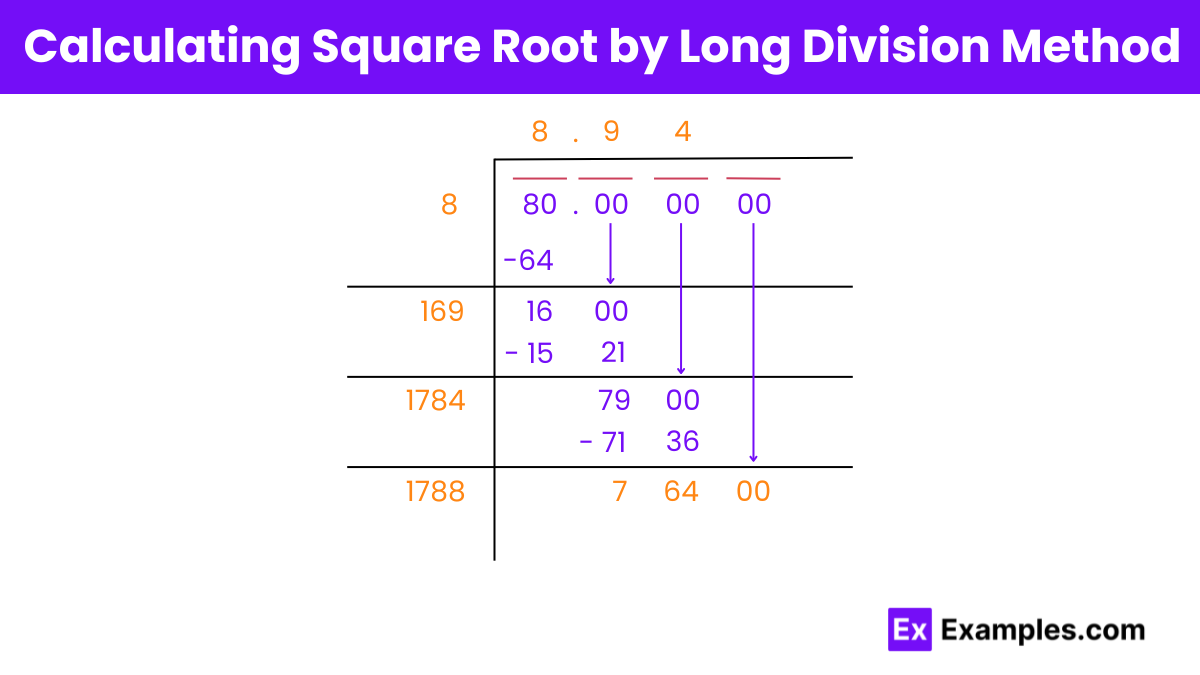
Finding the square root of 80 using the long division method can be made simple with these steps:
Start with 80: Write 80 down and put a bar over it. If you’re finding decimals, pair zeros in twos from left to right after the decimal point.
Find the largest square: Look for a number that squares to less than or equal to 80. Here, 8 works because 8 times 8 is 64. Subtract 64 from 80, leaving a remainder of 16.
Bring down zeros: Add a pair of zeros (making it 1600) to the remainder for more precision.
Double and guess: Take the quotient (8), double it (making 16), and put a space next to it for a new digit. Now, guess a digit (X) that makes 16X times X less than or equal to 1600. This is your next step in the division.
Continue for decimals: Keep repeating the process, adding pairs of zeros and guessing the next digit, to find the decimal part of the square root as precisely as you like.
This method helps you break down finding the square root of 80 into manageable steps, allowing you to get as close to the actual value as you need, even including decimal places.
A perfect square is a number that is the square of an integer, and since no integer squared equals 80, it cannot be considered a perfect square.
The term “perfect square” refers to numbers that are squares of integers. 80 is not a perfect square itself, but the closest perfect squares are 64 (8^2) and 81 (9^2).
No integer’s square is 80, but the square root of 80 (√80) is approximately 8.94. This means 8.94 squared, or 8.94^2, equals 80. This value is an irrational number.
The number closest to √80 is 9. The square root of 81 is exactly 9, and 81 is the perfect square nearest to 80. So, √80 is just slightly less than 9.
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What is the approximate square root of 80?
8.6
8.7
8.8
8.9
Which of the following is closest to the square of 8.9?
80
81
82
83
Simplify the expression √80.
4√5
8√2
16
10√2
Find the square of 80.
6
64
640
6400
What is the square root of 6400?
60
70
80
90
Determine the value of 8√10.
80
70
60
50
What is 80 divided by its square root?
9
8.9
9.1
8
What is the square of the square root of 80?
80
90
110
100
Find the value of (√80)².
160
130
110
80
Find the approximate value of (√80)² - 80.
0
1
2
3
Before you leave, take our quick quiz to enhance your learning!

