What is the square root of 90 rounded to the nearest whole number?
9
10
11
12

The square of 90, denoted as 90², equals 8100. To calculate it, you multiply 90 by itself. This operation reveals that 90 times 90 results in 8100, illustrating a basic concept in algebra where squaring a number means raising it to the power of two. Visually, if you imagine a square with each side measuring 90 units, the total area of that square would be 8100 square units. This concept is fundamental in mathematics, especially in geometry, where understanding squares helps in calculating areas and in various other applications where square values are used.
The square root of 90, denoted as √90, is approximately 9.4868. To compute it, you find the number which, when multiplied by itself, results in 90. In mathematical terms, finding the square root involves determining the number that, when raised to the power of 2, equals the original number. Visually, you can represent the square root of 90 as a square with sides of length approximately 9.4868 units, where the area of the square is 90 square units. Understanding square roots is crucial in various mathematical disciplines and real-world applications, such as geometry, algebra, and in scenarios where you need to determine the original dimensions from an area measurement. In practical situations, knowing the square root of 90 is useful for calculations involving the extraction of original quantities from squared values.
Exponential Form: 90^1/2 or 90^0.5
Radical Form: √90
This is because 90 cannot be expressed as the square of a rational number. In mathematical terms, an irrational number is one that cannot be written as a simple fraction a/b, where a and b are integers and b is not zero. The decimal expansion of an irrational number is non-repeating and non-terminating, and since no integer squared gives 90, √90 must be irrational.
Finding the value of the square root of 90 (√90) can be done through various methods, each suitable for different levels of precision and contexts:
1. Estimation
This method involves guessing and checking. You might start by recognizing that 92=8192=81 and 102=100102=100, placing √90 between 9 and 10. Fine-tune your estimate based on these bounds.
2. Using a Calculator
For most practical purposes, using a calculator is the quickest and most accurate method. Simply enter 90 and press the square root button to get an immediate and precise decimal value.
3. Long Division Method
This traditional method involves a step-by-step manual calculation that resembles long division. It can be very precise if carried out with enough decimal places, although it’s more time-consuming than using a calculator.
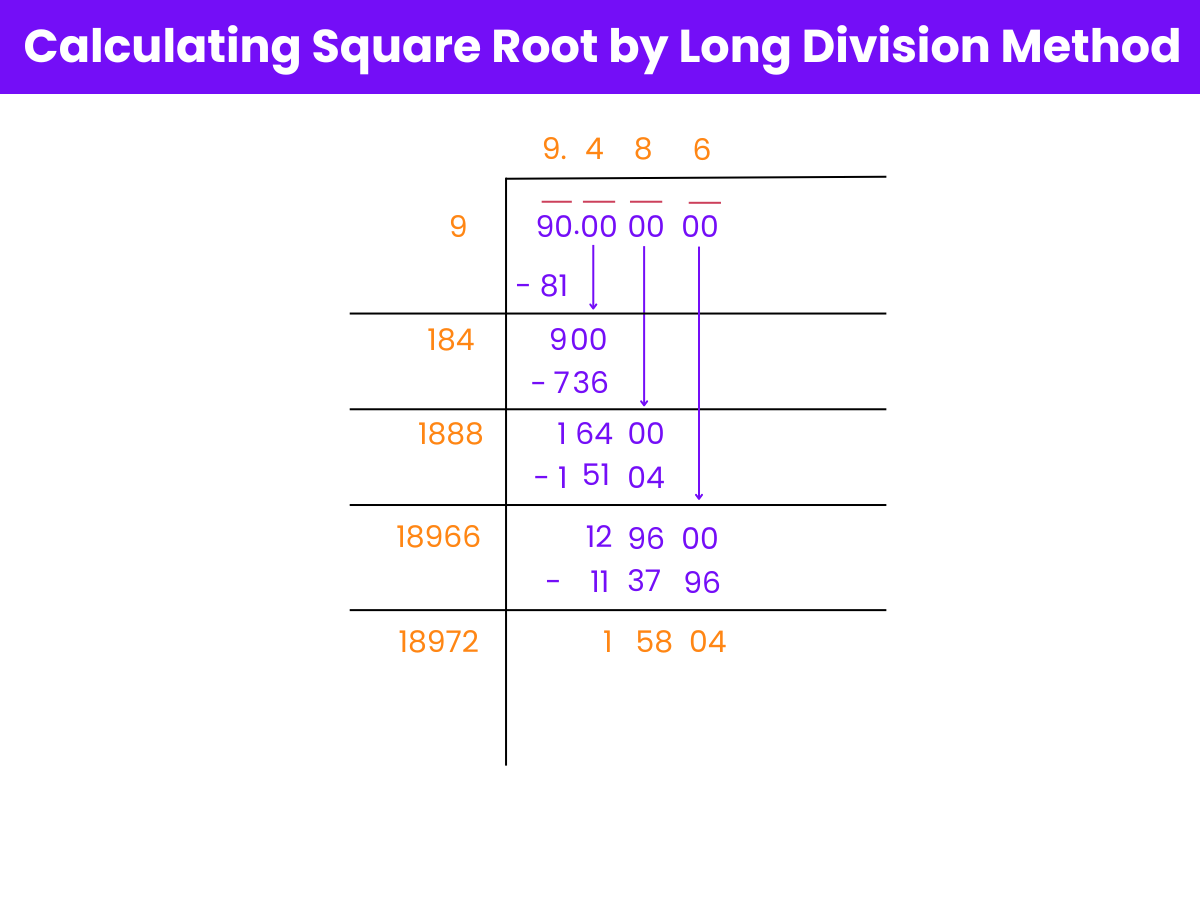
To find the square root of 90 using the long division method, follow these simplified steps:
Initial Setup: Write 90 as 90.00 00 00, breaking it into pairs of digits after the decimal point.
First Calculation: Find a number whose square is closest to 90 without exceeding it. Since 9×9=81, use 9. Subtract 81 from 90 to get a remainder of 9.
Extend the Division: Bring down the next pair of zeros, making the new dividend 900.
New Divisor Setup: Double the initial quotient (9), which is 18, and use it as the start of your new divisor (180).
Refine the Divisor: Find a digit to add to 180 to form a new divisor (184) such that 184×4=736 is as close as possible to 900 without exceeding it. Subtract 736 from 900 to get 164.
Repeat the Process: Bring down the next pair of zeros, making 16400 the new dividend. Continue this process, refining the quotient and divisor until the desired precision (three decimal places) is achieved.
Result: After these steps, the approximate square root of 90 is 9.486.
A perfect square is a number that can be expressed as the square of an integer. The square roots of 90 are not integers.
The square root of 90 lies between two integers: 9 and 10. Since 9²=81 and 10²=100, √90 is approximately 9.486, positioned between these two values.
Yes, the square root of 90 is a real number. It is an irrational number that can be approximately expressed but cannot be exactly represented as a simple fraction.
No, 90 is not a cube root. A cube root is a number that, when cubed (multiplied by itself three times), equals a given number. 90 does not fit this definition.
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What is the square root of 90 rounded to the nearest whole number?
9
10
11
12
What is the square of 90?
8100
810
9000
81,000
What is the approximate value of the square root of 90?
8.5
9
9.5
10
Which of the following is true about the square root of 90?
It is an integer
It is a rational number.
It is an irrational number
It is a whole number
What is the simplified radical form of the square root of 90?
\(3\sqrt{10}\)
\(3\sqrt{5}\)
\(6\sqrt{2}\)
\(5\sqrt{3}\)
If \( x = \sqrt{90} \), what is x2?
45
90
180
8100
Which of the following equations is correct?
\( \sqrt{90} = 10 \)
\( \sqrt{90} = 9 \)
\( \sqrt{90} = 3\sqrt{10} \)
\( \sqrt{90} = 6\sqrt{2} \)
What is the value of \( \sqrt{81} + \sqrt{9} \)?
12
10
15
9
Which pair of numbers is such that their product is 90 and their sum is 19?
9 and 10
15 and 6
10 and 9
18 and 5
If the area of a square is 90 square units, what is the length of each side of the square?
\( \sqrt{90} \) units
10 units
9 units
45 units
Before you leave, take our quick quiz to enhance your learning!

