Square & Square Root of 96
Square of 96
The square of 96 (96²) is calculated by multiplying 96 by itself:
96×96=9216.
So, the square of 96 is 9216.
Geometrically, if you have a square with each side measuring 96 units, the total area enclosed by the square will be 9216 square units.
Understanding the square of 96 is essential in various mathematical contexts, including geometry, algebra, and arithmetic. It finds applications in calculating areas, volumes, distances, and solving mathematical problems.
Square Root of 96
or
√796=9.798 up to three places of decimal
The square root of 96 (√96) is an irrational number, approximately equal to 9.79898987322.
It represents a number that, when multiplied by itself, results in 96:
√96≈9.7989898732296
Since 96 is not a perfect square, its square root cannot be simplified to a whole number or a simple fraction. Instead, it is a non-repeating, non-terminating decimal.
The square root of 96 finds applications in various fields such as mathematics, physics, engineering, and finance, where precise calculations are required.
Exponential Form: 96^½ or 96^0.5
Radical Form: √96
Is the Square Root of 96 Rational or Irrational?
- A rational number is any number that can be expressed as a fraction a/b where a and b are integers, and b is not equal to zero. It includes integers, fractions, and finite or repeating decimals.
- An irrational number is a real number that cannot be expressed as a simple fraction, and its decimal representation goes on infinitely without repeating.
Since 96 is not a perfect square, its square root cannot be expressed as a fraction of two integers. Additionally, the decimal representation of √96 is non-repeating and non-terminating. Therefore, √96 is classified as an irrational number.
The square root of 96 (√96) is irrational because it cannot be expressed as a simple fraction. Its decimal representation is non-repeating and non-terminating, indicating that it goes on infinitely without a pattern. Since 96 is not a perfect square, its square root cannot be simplified to a rational number. Therefore, √96 is classified as an irrational number in mathematics.
Methods to Find Value of Root 96
Estimation Method:
- Start by finding the nearest perfect squares around 96. In this case, the nearest perfect squares are √81 = 9 and √100 = 10.
- Since 96 is closer to 100, start with an initial estimate of √96 ≈ 9.5.
- Refine the estimate iteratively using trial and error until you reach a satisfactory approximation.
Long Division Method:
- Use the long division method to approximate the square root of 96 manually.
- Start with an initial guess, such as 9, and proceed with division and adjustment until you achieve the desired accuracy.
- This method involves a series of steps of trial and error to converge on an approximation of √96.
Newton’s Method:
- Apply Newton’s method, an iterative algorithm, to approximate the square root of 96.
- This method involves refining an initial guess through successive iterations until reaching a sufficiently accurate approximation.
- Newton’s method is more efficient but requires a deeper understanding of calculus and iterative algorithms.
Using a Calculator or Software:
- Utilize a scientific calculator or mathematical software to directly calculate the square root of 96.
- Input 96 into the calculator or software, and the result will provide the accurate value of √96.
Square Root of 96 by Long Division Method
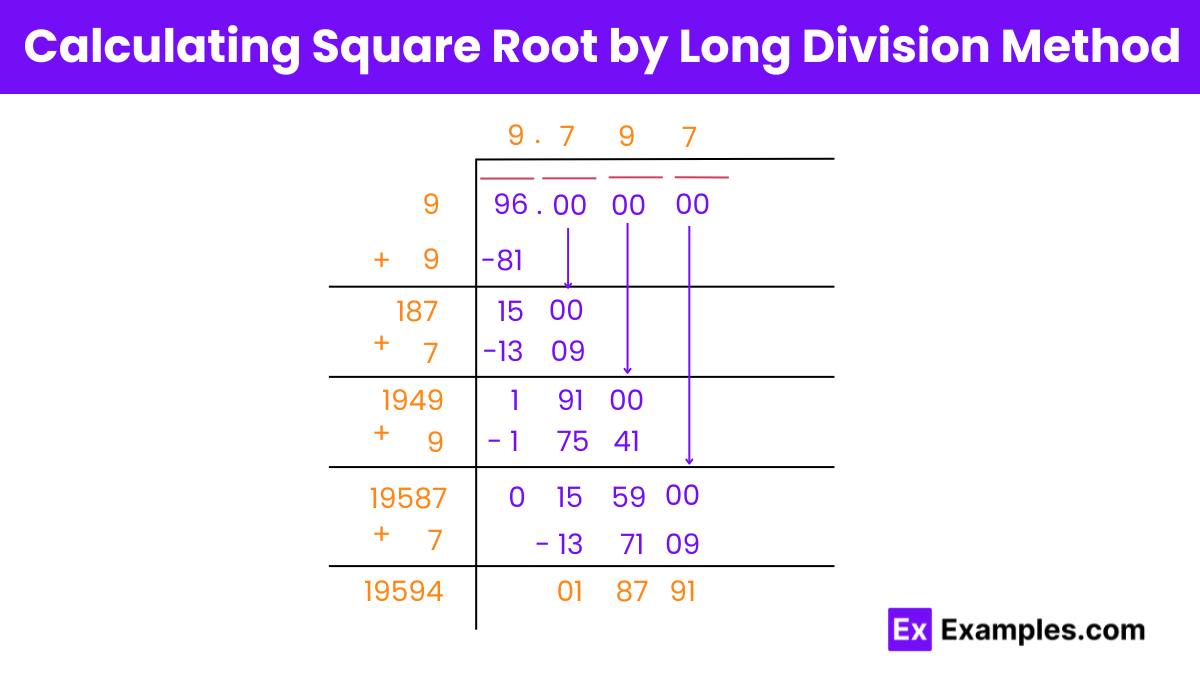
Here’s an alternative presentation of the steps to find the square root of 96 using the long division method:
Digit Pairing: Pair off the digits of the number 96, starting from the right, and place a horizontal bar to indicate pairing.
Initial Estimation: Find a number that, when squared, gives a value less than or equal to 96. In this case, 9 fits as 9×9 = 81. Therefore, the initial quotient and divisor are both 9.
Iteration: Subtract the square of the current divisor from the paired digits to obtain the remainder. Bring down the next pair of digits and continue the process iteratively.
Decimal Placement: Place a decimal point in the quotient and dividend after the whole number part. Add pairs of zeros to the dividend after the decimal point for every pair of digits brought down.
Adjustment: Determine the next digit of the quotient by finding the largest digit that, when appended to the current divisor, gives a product less than or equal to the current remainder. Repeat this process until the desired level of precision is achieved.
Repeat:Continue the steps of bringing down digits, subtracting squares, and finding the next digit of the quotient until all the digits of the square root are determined.
By following these steps iteratively, the square root of 96 can be approximated using the long division method.
96 is Perfect Square root or Not
A perfect square is a number that can be expressed as the square of an integer. In other words, it is the product of an integer multiplied by itself. For example, 25 is a perfect square because it equals 5×5.
However, 96 cannot be expressed as the product of an integer multiplied by itself. Therefore, it is not a perfect square.
FAQ’s
What are the practical applications of the square root of 96?
The square root of 96 has applications in fields such as mathematics, physics, engineering, and finance, where precise calculations are required.
Are there any interesting mathematical properties associated with the number 96?
Yes, 96 has various mathematical properties and relationships with other numbers, which can be explored in algebraic, geometric, or numerical contexts.
How does understanding the square root of 96 contribute to problem-solving in real-life situations?
Understanding the square root of 96 and its properties can help in solving practical problems involving measurements, dimensions, areas, volumes, and other quantitative aspects in fields such as construction, engineering, finance, and statistics.
Share :
