Square & Square Root of 99
Square & Square Root of 99
Square of 99
The square of 99 can be calculated by multiplying the number by itself:
Therefore, the square Numbers of 99 is 9801. This operation involves simple multiplication, which can be done using a calculator, through long multiplication by hand, or using mental math techniques if you’re skilled with numbers.
Square Root of 99
The square root of 99, denoted as √99 represents the value which, when multiplied by itself, yields 99. Like the square root of 192 and many other non-perfect squares, the square root of 99 is an irrational number. This means its decimal expansion is non-repeating and infinite. When calculated, √99 is approximately 9.9498743710662.
Due to its irrational nature, the square root of 99 does not have a simple, finite decimal form. It’s an important concept in various mathematical fields, geometric calculations, and practical applications, particularly in disciplines that require precision, such as engineering, physics, and advanced mathematics. Understanding the properties and calculation of such square roots can be crucial for accurate problem solving and analysis in these fields.
Square Root of 99: 9.9498743710662
Exponential Form: 99^½ or 99^0.5
Radical Form: √99
Is the Square Root of 99 Rational or Irrational?
This means it cannot be expressed exactly as a simple fraction because its decimal expansion goes on forever without repeating. The number 99 is not a perfect square (no integer multiplied by itself equals 99), which is why its square root results in an irrational number. This characteristic is typical for the square roots of most numbers that are not perfect squares.
Method to Find Value of Root 99
To find the square root of 99, you can use several different methods, each with its own benefits depending on your need for speed, simplicity, or precision. Here’s a clearer explanation of some common techniques:
1. Estimation Method:
Identify close squares: Recognize that 9² = 81 and 10² = 100.
Since 99 is between these two squares, its square root must be between 9 and 10.
Refine the guess: Estimate that the square root of 99 is closer to 10 because 99 is very close to 100. You might guess 9.9 or 9.95 and refine from there by trying smaller adjustments.
2. Calculator Method:
Direct calculation: Simply use a calculator to find the square root. Typing in “√99” or “99^(0.5)” will give you a precise decimal result immediately.
3. Long Division Method:
Setup: Write down 99 as 99.0000, extending it with zeros for more precision if needed.
Divide: Find the largest whole number whose square is less than or equal to 99 (9 in this case). Subtract
9² (81) from 99 to get 18.
Bring down and continue: Bring down two zeros to make it 1800. Find the next digit of the root by setting up a trial multiplication that fits into 1800. This process resembles long division but incorporates multiplication to refine the guess.
4. Graphical Method (using technology):
Graph the function: Use graphing software or a graphing calculator to plot y=x² Find the root: Look for the y=99 intersects the curve. The x-coordinate at this intersection is the square root of 99.
Each of these methods will help you understand or calculate the square root of 99. The choice of method depends on the tools you have available and how precise you need the answer to be.
Square Root of 99 by Long Division Method
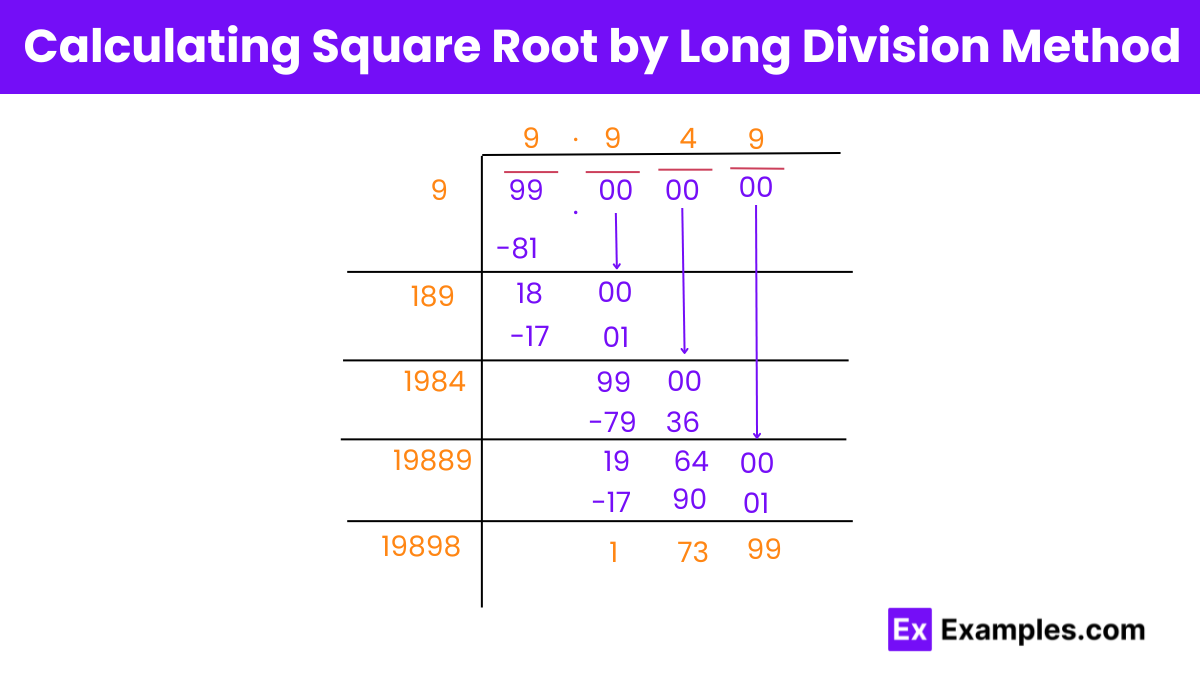
Initiate with 99.000000: Treat 99 as ‘99.000000’ for precision purposes.
Step 1: First Division Operation: Dividing 99 into pairs (from the right), the first pair is 99. The first operation uses 9 as both the quotient and divisor because 9 × 9 = 81, which is subtracted from 99 to get a remainder of 18.
Step 2: Double the Quotient: Doubling the quotient (9) gives 18. This will be used to modify the divisor in the next step.
Step 3: Bring Down Zeros: Apply a decimal point after the quotient (9.), bringing down two zeros makes it 1800.
Next Calculation: Choosing 9 to add to 180 (the doubled quotient) makes the new divisor 189. 189 × 9 = 1701, subtracted from 1800 results in a remainder of 99.
Step 5: Doubling the Quotient First, take the quotient from the previous steps, which is 99, and double it. This gives us 198. Now, set 1980 as the new divisor.
Next, determine a digit to place in the unit’s place such that when this new number (formed by appending the digit to 198) is multiplied by the digit itself, the product is less than or equal to the current dividend.
Here, appending 4 to 198 (making 1984) and multiplying it by 4 results in 7936, which is less than our working dividend of 9900.
Step 6: Calculating the Remainder and Continuing the Process Subtract the product (7936) from the current dividend (9900) to get the remainder, which is 1964.
Bring down the next pair of zeros (if calculating for more precision) and continue the process similar to steps above until you achieve the desired precision in the square root calculation.
Repeat these steps, adjusting the new divisor and finding the next digit until the quotient is stable to two decimal places.
99 is Perfect Square root or Not?
A perfect square is a number that can be expressed as the product of an integer with itself. For instance, 81 is a perfect square because it can be written as 9 × 9 . However, the square root of 99 is approximately 9.949, which is not an integer. Therefore, 99 cannot be expressed as the square of any integer, and thus it is not a perfect square.
FAQ’S
What is the simplest form of √ 99?
The simplest form of √99 can be expressed as 3√11.
How can you find the square root of 99 without a calculator?
You can estimate the square root of 99 by using methods like the long division method or by iterative approximation methods such as the Newton-Raphson method.
Share :
